問題文
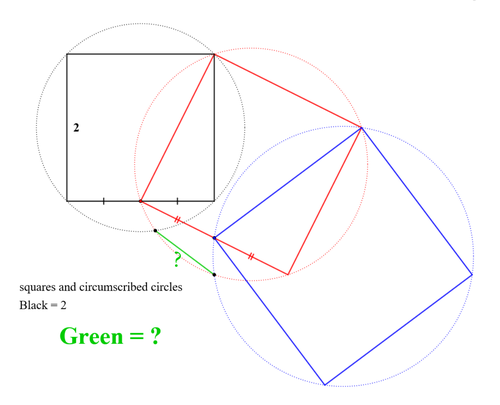
図のように黒・赤・青の正方形と、その外接円が配置されています。黒い正方形の一辺の長さが2であるとき、緑で示した線分の長さを求めてください。
解答形式
半角数字で解答してください。
問題文
※2020.11.10 18:49 問題タイトルを修正しました。
(解答に影響はありません)
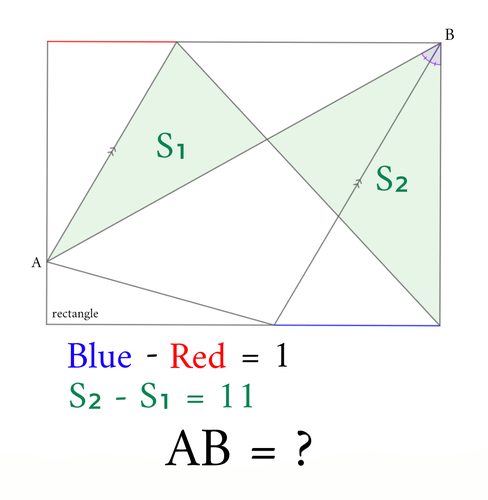
図中の線分ABの長さを求めてください。
緑で示した2つの三角形の面積の差は11,赤と青で示した線分の長さの差は1です。
解答形式
半角数字で解答してください。
問題文
△ABCにおいて、垂心をH、外心をOとするとAB//HOであった。このとき、∠Cの角度としてあり得る値の範囲を求めてください。
ただし、OとHが一致する場合は除きます。
解答形式
∠Cの範囲は度数法で表すと、$(0°<)\alpha°<C<\beta°(<180°)$となります。
$\alpha+\beta$を半角数字で解答してください。
問題文
$x_1,x_2,\ldots,x_{24}$は正の実数とします。このとき、次の式の最小値を求めてください。
$$
\left(\sum_{n=1}^{24}\frac{n}{x_n}\right)\times\left(\sum_{n=1}^{24}nx_n\right)
$$
解答形式
半角数字で解答してください。
問題文
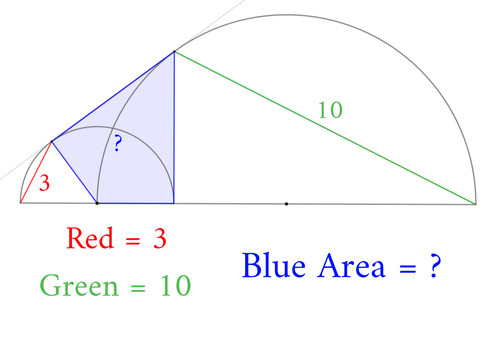
図のように2つの半円が配置されています。(右側の半円の直径の一端は左側の半円の中心に一致する。)赤、緑で示した線分の長さがそれぞれ3,10のとき、青で示した四角形の面積を求めてください。
ただし、図中点線で示した直線は2つの半円の共通接線です。
解答形式
半角数字で解答してください。
問題文
【解答形式に注意!】
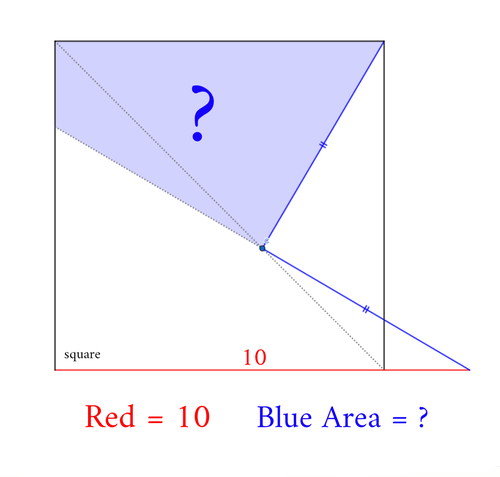
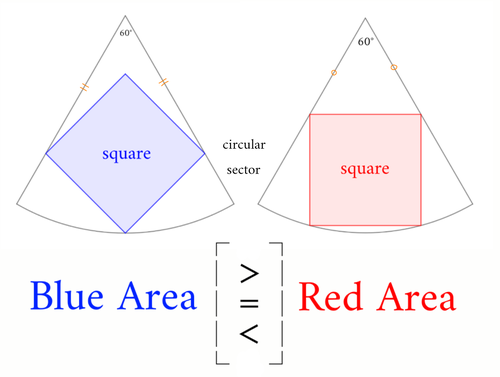
半径と中心角が等しい扇形に正方形が内接しています。青い正方形と赤い正方形の面積の大小関係を調べてください。
ただし、同じ印をつけた部分の長さは等しいです。
解答形式
(青の面積) > (赤の面積) なら 1
(青の面積) = (赤の面積) なら 2
(青の面積) < (赤の面積) なら 3
を、半角数字で解答してください。
問題文
$△ABC$は鋭角三角形とします。次に、$A,B,C$から$BC,CA,AB$におろした垂線の足をそれぞれ$X,Y,Z$とし、$△ABC,△XYZ$の内接円の半径をそれぞれ$r,r'$とします。このとき、次の式の最小値を求めてください。
$$
\frac{r}{r'}\cos{\frac A2}\cos{\frac B2}\cos{\frac C2}
$$
解答形式
$$
\frac{r}{r'}\cos{\frac A2}\cos{\frac B2}\cos{\frac C2}\geq\frac{[ア]\sqrt{[イ]}}{[ウ]}=(最小値)
$$
となります。$[ア]+[イ]+[ウ]$を半角数字で解答してください。
ただし、$[ア],[イ],[ウ]$には自然数が入ります。また、分数部分は既約分数に、根号内の数字は最小となるようにしてください。
問題文
三角形の3つの内角の大きさを$A,B,C$とします。このとき、次の式の最小値を求めてください。
$$
\frac{1-\cos A}{\cos B+\cos C}+\frac{1-\cos B}{\cos C+\cos A}+\frac{1-\cos C}{\cos A+\cos B}
$$
解答形式
最小値は$\frac {[ア]}{[イ]}$となります。$[ア]+[イ]$を解答してください。
ただし、$[ア],[イ]$にはそれぞれ自然数が入り、その最大公約数は$1$とします。
問題文
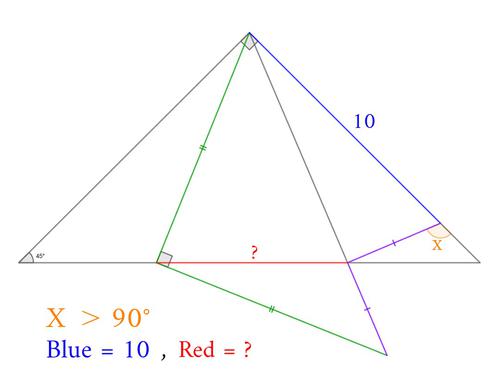
2つの直角二等辺三角形が、それらの斜辺が交点をもつように配置されています。青い線分の長さが10、Xで示した角が鈍角のとき、赤い線分の長さを求めてください。
ただし、同じ色で示した線分の長さはそれぞれ等しいです。
解答形式
(赤い線分の長さ)$=[ア]\sqrt{[イ]}$ となります。
ただし、$[ア],[イ]$にはそれぞれ自然数が入ります。$[ア]+[イ]$を解答してください。また、$[イ]$に入る自然数はできるだけ小さくしてください。
例: (赤い線分の長さ)$=3\sqrt5$ なら、$3+5\rightarrow8$と解答
問題文
(2020.9.26 11:57追記)
解答形式に不備があったため、訂正致しました。
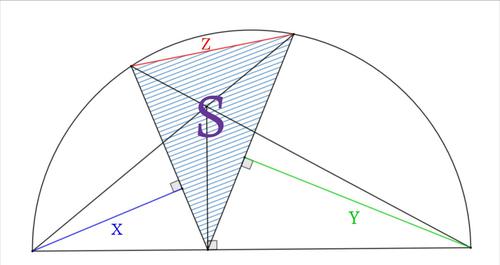
図の青、緑、赤の線分の長さを$X,Y,Z$、斜線部の面積を$S$とすると、次の式が成り立つ。
$$
\frac{[ア]}{S}=\frac{[イ]}{Z}\left(\frac{1}{X}+\frac{1}{Y}\right)
$$
なお、図の曲線は半円の弧である。
解答形式
$[ア],[イ]$にはともに自然数が入ります。その和を半角数字で解答してください。
ただし、その和が最小となるように解答してください。
例:$[ア]=4,[イ]=2$なら$6$ではなく(両辺を$2$で割ることにより)$3$と解答。
問題文
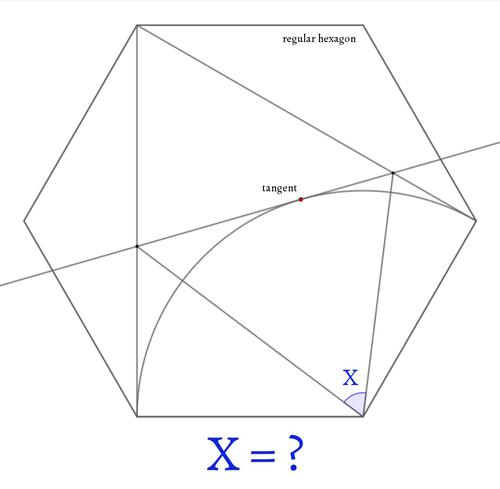
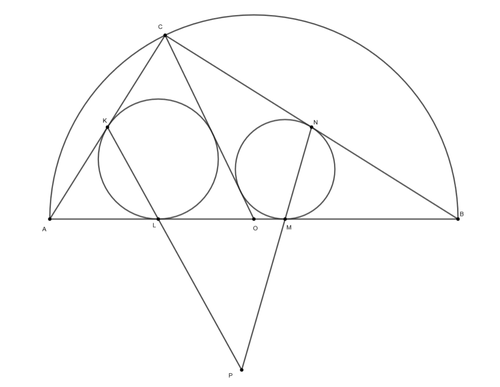
図のように正六角形・扇形・その接線があります。Xで示した角の大きさを求めてください。
解答形式
0以上360未満の半角数字で解答してください。
※単位(°や度など)をつけず、度数法で解答。
問題文
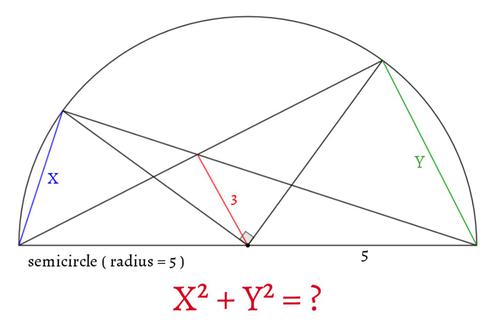
図のように配置された図形で、半円の半径が$5$、赤、青、緑の線分の長さがそれぞれ$3,X,Y$のとき、$X^2+Y^2$の値を求めてください。
解答形式
半角数字で解答してください。
問題文
問題文を3つの半円が図のように配置されています。赤い部分の面積が9、緑の部分の面積が5のとき、青い部分の面積を求めてください。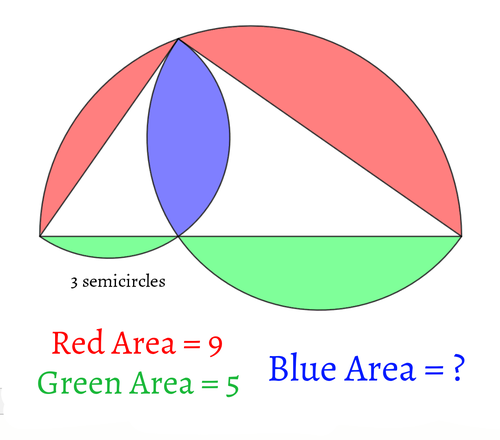
解答形式
半角数字で解答してください。
問題文
※解答形式に注意!
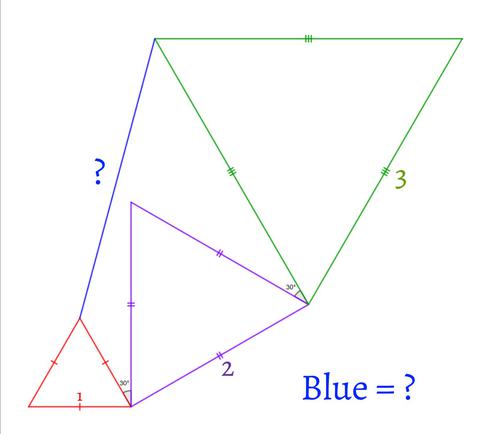
図のように配置された3つの正三角形があります。青い線分の長さを求めてください。
ただし、赤、紫、緑の線分の長さはそれぞれ1,2,3で、隣り合う正三角形の間の角は30°です。
解答形式
答えは自然数$A,B$を用いて$A\sqrt{B}$の形に表せます。$A+B$を解答してください。
ただし、根号の中はできるだけ小さい自然数にしてください。
問題文
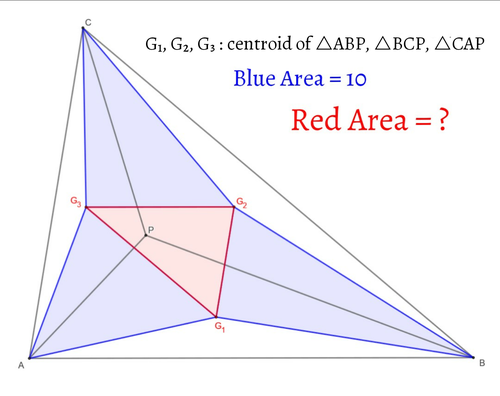
△ABCと点Pをとり、△ABP, △BCP, △CAPの重心をそれぞれ$G_1, G_2, G_3$とします。青で示した3つの三角形の面積の和が10のとき、$△G_1G_2G_3$(赤い三角形)の面積を求めてください。
解答形式
半角数字で解答してください。
問題文
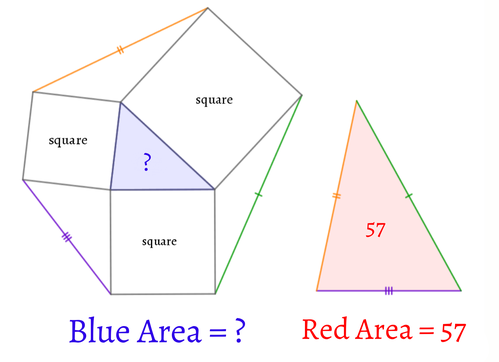
三角形の外側に3つの正方形を図のように作りました。橙・緑・紫の線分の長さを3辺の長さとする三角形(赤い三角形)の面積が57のとき、元の三角形(青い三角形)の面積を求めてください。
解答形式
半角数字で解答してください。