整角問題

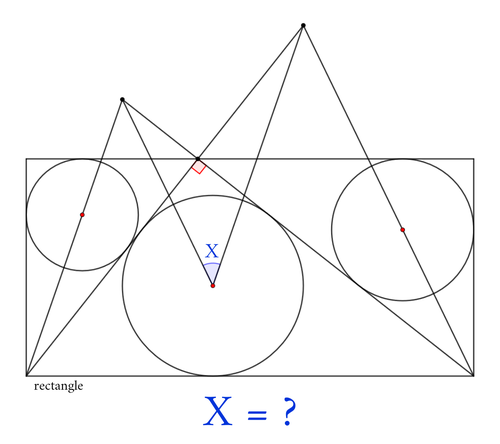
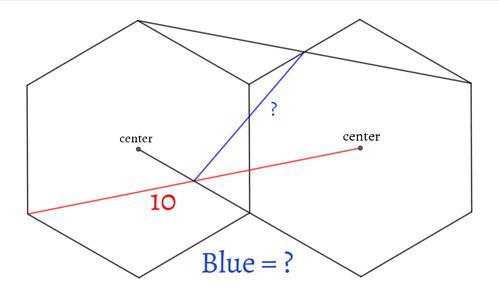
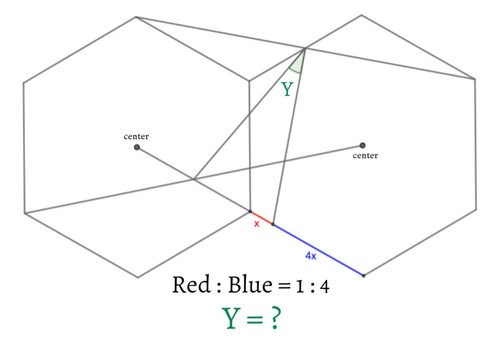
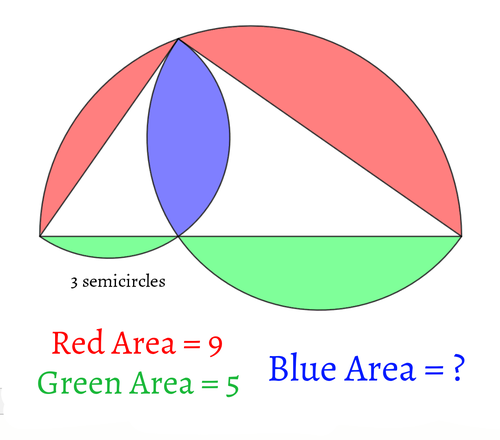
解説

辺$BC$上に，$\angle PDC=138^\circ$なる点$D$をとる．このとき，$\angle PDB=180^\circ-\angle PDC=42^\circ$．
また，線分$DP$の$P$側の延長上に，$\angle PCE=6^\circ$なる点$E$，および$\angle PCF=18^\circ$なる点$F$をそれぞれとる．このとき，
$\angle ECB=\angle BCP+\angle ECP=18^\circ$，
$\angle DCF=\angle DCP+\angle PCE+\angle ECF=30^\circ$，
$\angle DFC=180^\circ-\angle DCF-\angle FDC=12^\circ$，
$\angle CED=\angle ECF+\angle EFC=24^\circ$．
ここに，$\angle ECF=\angle EFC$だから，$EC=EF$である．
さて，三角形$CDF$の外心を$G$とする．このとき，$\angle DGF=2\angle DCF=60^\circ$だから，三角形$DFG$は正三角形で，$DF=DG=GF$，$\angle FDG=\angle EFG=60^\circ$．
また，$\angle GDC=\angle FDC-\angle FDG=78^\circ$で，これと$GD=GC$より，$\angle GCD=\angle GDC=78^\circ$だから，$\angle DGC=180^\circ-\angle GDC-\angle GCD=24^\circ$．
一方，$EG$共通，$EC=EF$，$GC=GF$から，2点$C,F$は，直線$EG$を軸として対称の位置にある．したがって，$\angle FGE=\angle CGE=\dfrac{\angle DGF+\angle DGC}{2}=42^\circ$，$\angle FEG=180^\circ-\angle EFG-\angle FGE=78^\circ$．
次に，直線$EG$上に，$\angle GHC=42^\circ$なる点$H$をとる．このとき，$\angle GCH=180^\circ-\angle HGC-\angle GHC=96^\circ$，
$\angle HCB=\angle GCH-\angle GCB=18^\circ$．
また，対称性より，$\angle HFE=\angle HCE=\angle HCB+\angle ECB=36^\circ$，$FH=FG=FD$．これより，三角形$FHD$は二等辺三角形だから，$\angle FDH=\dfrac{180^\circ-\angle HFD}{2}=72^\circ$，$\angle HDB=\angle FDH-\angle FDB=30^\circ$．
したがって，$\angle CHD=\angle HDB-\angle HCD=12^\circ$．
直線$CB$上に，$\angle CHI=30^\circ$なる点$I$をとる．このとき，$\angle EHI=\angle CHG-\angle CHI=12^\circ=\angle CHD$，$\angle HCI=\angle ECD$より，
$I$は，三角形$ECH$における$D$の等角共役点である．したがって，$\angle HEI=\angle CED=24^\circ$．
このとき，$\angle EIH=180^\circ-\angle EHI-\angle HEI=144^\circ=180^\circ-\angle HFE$．
よって，内接四角形の定理の逆より，四角形$EFHI$は円に内接する．したがって，円周角の定理より，$\angle IFE=\angle IHE=12^\circ$，$\angle FIE=\angle FHE=42^\circ$．
ここに，$\angle IFP=\angle CFE$，$\angle BCP=\angle FCE$より，$P$は，三角形$FIC$における$E$の等角共役点である．したがって，$\angle CIP=\angle FIE=42^\circ$．
以上より，$\angle CIP=\angle CBP$だから，$I$は$B$に一致する．このとき，$\angle EBP=180^\circ-\angle BFP-\angle FPB-\angle CBP-\angle FBE=42^\circ$であるから，
$E$は$A$に一致する．
したがって，$\angle BAP=\angle BFA+\angle FBA=\boldsymbol{54^\circ}$

【別解】
直線$AP$と辺$BC$との交点を$D$とし，$\angle CPD=\theta$とおく．
このとき，$\angle PAC=\angle CPD-\angle ACP=\theta-6^\circ$
$\angle ADB=\angle BCP+\angle CPD=12^\circ+\theta$
$\angle BAD=180^\circ-\angle ABC-\angle ADB=84^\circ-\theta$
いま，正弦定理より
$\dfrac{AB}{\sin\left(12^\circ+\theta \right)}=\dfrac{BD}{\sin\left(84^\circ-\theta \right)}\Leftrightarrow\dfrac{AB}{BD}=\dfrac{\sin\left(12^\circ+\theta \right)}{\sin\left(84^\circ-\theta \right)}$
一方，$\angle ABP=\angle DBP$より，$\dfrac{AP}{PD}=\dfrac{AB}{BD}=\dfrac{\sin\left(12^\circ+\theta \right)}{\sin\left(84^\circ-\theta \right)}$　…①
また，$\dfrac{AP}{\sin 6^\circ}=\dfrac{CP}{\sin\left(\theta-6^\circ \right)}\Leftrightarrow CP=\dfrac{\sin\left(\theta-6^\circ \right)}{\sin 6^\circ}AP$　…②
$\dfrac{PD}{\sin 12^\circ}=\dfrac{CP}{\sin\left(12^\circ+\theta \right)}\Leftrightarrow CP=\dfrac{\sin\left(12^\circ+\theta \right)}{\sin 12^\circ}PD$　…③
②，③より
$\dfrac{\sin\left(\theta-6^\circ \right)}{\sin 6^\circ}AP=\dfrac{\sin\left(12^\circ+\theta \right)}{\sin 12^\circ}PD\Leftrightarrow\dfrac{AP}{PD}=\dfrac{\sin 6^\circ\sin\left(12^\circ+\theta \right)}{\sin 12^\circ\sin\left(\theta-6^\circ \right)}$　…④
①，④より，$\dfrac{\sin\left(12^\circ+\theta \right)}{\sin\left(84^\circ-\theta \right)}=\dfrac{\sin 6^\circ\sin\left(12^\circ+\theta \right)}{\sin 12^\circ\sin\left(\theta-6^\circ \right)}$
したがって，$\sin 12^\circ\sin\left(\theta-6^\circ \right)=\sin6^\circ\sin\left(84^\circ-\theta \right)$
ここに，
$\sin 12^\circ=2\sin 6^\circ\cos 6^\circ$
$\sin\left(\theta-6^\circ \right)=\sin\theta\cos 6^\circ-\cos\theta\sin 6^\circ$
$\sin\left(84^\circ-\theta \right)=\cos\left(6^\circ+\theta \right)=\cos 6^\circ\cos\theta-\sin 6^\circ\sin\theta$
より，
$2\sin 6^\circ\cos 6^\circ\left(\sin\theta\cos6^\circ-\cos\theta\sin 6^\circ \right)=\sin 6^\circ\left(\cos 6^\circ\cos\theta-\sin 6^\circ\sin\theta \right)$
$\Leftrightarrow\sin\theta\left(\sin 6^\circ+2\cos^2 6^\circ\right)=\cos\theta\left(2\sin 6^\circ\cos 6^\circ+\cos 6^\circ \right)$
よって，
$\tan\theta=\dfrac{\sin\theta}{\cos\theta}=\dfrac{2\sin 6^\circ\cos 6^\circ+\cos 6^\circ}{\sin 6^\circ+2\cos^2 6^\circ}$
ここで，次の補題を示す．
$\boldsymbol{補題．}$$\sin 54^\circ=\dfrac{1+\sqrt{5}}{2}$，$\cos 54^\circ=\dfrac{\sqrt{5-\sqrt{5}}}{2\sqrt{2}}$
$\boldsymbol{証明．}$$EF=EG$，$\angle FEG=108^\circ$なる$\triangle EFG$をつくる．このとき，
$\angle EFG=\dfrac{180^\circ-\angle FEG}{2}=36^\circ$
また，辺$FG$上に，$EH=FH$なる点$H$をとる．このとき，$\angle HEF=\angle HFE=36^\circ$より，$\angle EHG=\angle HEF+\angle HFE=72^\circ$
一方，$\angle HEG=\angle FEG-\angle HEF=72^\circ$
したがって，$\angle EHG=\angle HEG$だから，$GH=GE$
ここに，$FHE=180^\circ-\angle EHG=108^\circ=\angle FEG$，$HF:EF=HE:EG$より，二辺比夾角相等から，$\triangle HFE\sim\triangle EFG$
したがって，$HF:EF=FE:FG$
ここに，$HE=HF=1$，$EF=EG=GH=x$とおくと，
$1:x=x:\left(1+x\right)$
これを解くと，$x=\dfrac{1\pm\sqrt{5}}{2}$で，$x>0$より，$x=\dfrac{1+\sqrt{5}}{2}$
さて，辺$EF$の中点を$M$とすると，$HM\perp EF$，$\angle EHM=\dfrac{1}{2}\angle EHF=54^\circ$．
このとき，$EM=\dfrac{1}{2}EF=\dfrac{1}{2}x=\dfrac{1+\sqrt{5}}{4}$だから，
$\sin 54^\circ=\dfrac{EM}{EH}=\dfrac{1+\sqrt{5}}{4}$
また，$\cos 54^\circ=\sqrt{1-\sin^{2} 54^\circ}=\sqrt{1-\left(\dfrac{1+\sqrt{5}}{4}\right)^{2}}=\dfrac{\sqrt{5-\sqrt{5}}}{2\sqrt{2}}　\square$
よって，補題より，
$\sin 6^\circ=\sin\left(60^\circ-54^\circ\right)=\sin 60^\circ\cos 54^\circ-\cos 60^\circ\sin 54^\circ=\dfrac{\sqrt{3}\sqrt{5-\sqrt{5}}}{4\sqrt{2}}-\dfrac{1+\sqrt{5}}{8}$
$\cos 6^\circ=\cos\left(60^\circ-54^\circ\right)=\sin 60^\circ\sin 54^\circ+\cos 60^\circ\cos 54^\circ=\dfrac{\sqrt{3}+\sqrt{15}}{8}+\dfrac{\sqrt{5-\sqrt{5}}}{4\sqrt{2}}$
したがって，
$2\sin 6^\circ\cos 6^\circ+\cos 6^\circ$
$=2\left(\dfrac{\sqrt{3}\sqrt{5-\sqrt{5}}}{4\sqrt{2}}-\dfrac{1+\sqrt{5}}{8}\right)\left(\dfrac{\sqrt{3}+\sqrt{15}}{8}+\dfrac{\sqrt{5-\sqrt{5}}}{4\sqrt{2}}\right)+\left(\dfrac{\sqrt{3}+\sqrt{15}}{8}+\dfrac{\sqrt{5-\sqrt{5}}}{4\sqrt{2}}\right)$
$=\dfrac{\sqrt{3}}{4}+\dfrac{\left(3+\sqrt{5}\right)\sqrt{5-\sqrt{5}}}{8\sqrt{2}}$
$\sin 6^\circ+2\cos^{2}6^\circ$
$=\left(\dfrac{\sqrt{3}\sqrt{5-\sqrt{5}}}{4\sqrt{2}}-\dfrac{1+\sqrt{5}}{8}\right)+2\left(\dfrac{\sqrt{3}\left(1+\sqrt{5}\right)}{8}+\dfrac{\sqrt{5-\sqrt{5}}}{4\sqrt{2}}\right)^{2}$
$=\dfrac{3}{4}+\dfrac{\sqrt{3}\left(3+\sqrt{5}\right)\sqrt{5-\sqrt{5}}}{8\sqrt{2}}$
より，
$\tan\theta=\dfrac{1}{\sqrt{3}}$
このとき，$\theta=30^\circ$だから，$\angle BAP=84^\circ-\theta=\boldsymbol{54^\circ}$