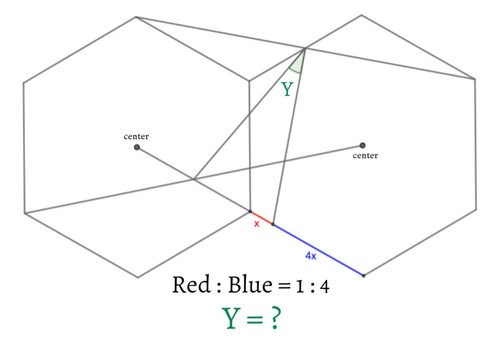
この問題はコンテスト「数学思考力テスト 第1回」の問題です。
ある座標平面がある。
(6、2)(6、0)(8、0)(8、18)(0、18)(0、2)(0、0)をそれぞれ
点A B C D E F G とする。この時、四角形ABGFと六角形DCBAFEの面積をそれぞれ2等分する直線Lを引くことを考える。
直線Lのy切片の絶対値を求めよ。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています