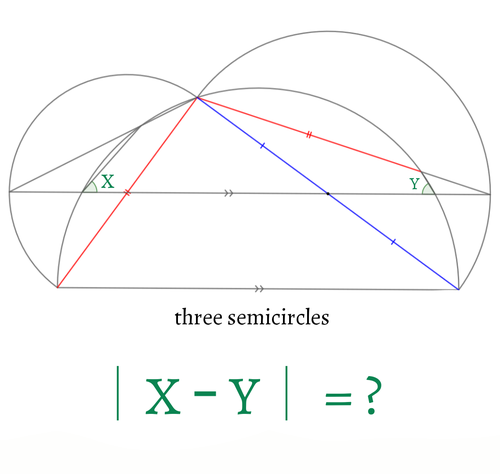
この問題はコンテスト「数学思考力テスト 第1回」の問題です。
全 14 件
| 回答日時 | 問題 | 解答者 | 結果 | |
|---|---|---|---|---|
| 2024年9月14日21:03 | 問題❶ |
|
正解
|
|
| 2024年9月14日21:03 | 問題❶ |
|
正解
|
|
| 2024年9月14日21:02 | 問題❶ |
|
正解
|
|
| 2024年9月14日21:02 | 問題❶ |
|
正解
|
|
| 2024年9月14日21:02 | 問題❶ |
|
正解
|
|
| 2024年9月14日21:02 | 問題❶ |
|
不正解
|
|
| 2024年3月27日15:58 | 問題❶ |
|
正解
|
|
| 2024年3月27日15:58 | 問題❶ |
|
正解
|
|
| 2024年2月4日13:49 | 問題❶ |
|
正解
|
|
| 2024年2月3日20:07 | 問題❶ |
|
正解
|
|
| 2023年8月25日19:56 | 問題❶ |
|
正解
|
|
| 2023年3月27日16:13 | 問題❶ |
|
正解
|
|
| 2023年3月27日1:01 | 問題❶ |
|
正解
|
|
| 2023年3月26日19:13 | 問題❶ |
|
不正解
|
おすすめ問題
この問題を解いた人はこんな問題も解いています