[B] 四次元モノサシ
解答
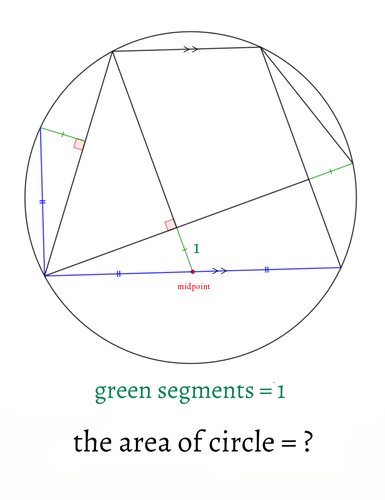
$\mathrm{AB}=\mathrm{AC}=p, \mathrm{AD}=q$ とおく。三角形 $\mathrm {ABD}, \mathrm {ACD}$ において、それぞれ $\angle \mathrm{BAD}=135^\circ, \angle \mathrm{CAD}=45^\circ$ であることに注意して余弦定理を用いると
\begin{eqnarray}
\mathrm{BD}^2 &=& \mathrm{AB}^2 +\mathrm{AD}^2 -2\mathrm{AB}\cdot\mathrm{AD}\cdot\cos{\angle \mathrm{BAD}} \\
&=&p^2+q^2+\sqrt{2}pq, \\
\mathrm{CD}^2 &=& \mathrm{AC}^2 +\mathrm{AD}^2 -2\mathrm{AC}\cdot\mathrm{AD}\cdot\cos{\angle \mathrm{CAD}} \\
&=& p^2+q^2-\sqrt{2}pq \\
\end{eqnarray}
であり、辺々掛け合わせると
\begin{eqnarray}
\mathrm{BD}^2 \cdot \mathrm{CD}^2 &=& (p^2+q^2+\sqrt{2}pq)(p^2+q^2-\sqrt{2}pq) \\
&=& (p^2+q^2)^2-2p^2q^2 \\
&=& p^4+q^4 \\
&=& \mathrm{AB}^4 + \mathrm{AD}^4
\end{eqnarray}
となる。したがって $\mathrm{AB}^4 + \mathrm{AD}^4= \mathrm{BD}^2 \cdot \mathrm{CD}^2 =10^2\cdot7^2=4900$ であり、$\fbox{アイウエ}=4900$ が答えとなる。
三角関数を使わない別解
線分 $\mathrm{BC}$ の中点を $\mathrm{M}$、点 $\mathrm{D}$ から直線 $\mathrm{BC}$ に下ろした垂線の足を点 $\mathrm{H}$ とする。 $\mathrm{AM}=\mathrm{BM}=\mathrm{CM}=\mathrm{DH}=r,\ \mathrm{AD}=\mathrm{MH}=q$ とおくと、
\begin{eqnarray}
\mathrm{AB}^4 + \mathrm{AD}^4 &=& (\sqrt{2}r)^4 + q^4 \\
&=& 4r^4+q^4 \\
&=& 4r^4+4r^2q^2+q^4-4r^2q^2 \\
&=& (2r^2 + q^2)^2 -4r^2q^2 \\
&=& (2r^2 + q^2 + 2rq)(2r^2 + q^2 - 2rq) \\
&=& ( r^2+(r+q)^2)( r^2+(r-q)^2) \\
\end{eqnarray}
である。
直角三角形 $\mathrm {BDH}, \mathrm {CDH}$ で、$\mathrm{DH}=r,\ \mathrm{BH}=\mathrm{BM}+\mathrm{MH}=r+q,\ \mathrm{CH}=|\mathrm{CM}-\mathrm{MH}| =|r-q|$ であり、それぞれに三平方の定理を用いることで
\begin{eqnarray}
r^2+(r+q)^2&=&\mathrm{DH}^2 + \mathrm{BH}^2 = \mathrm{BD}^2 \\
r^2+(r-q)^2&=&\mathrm{DH}^2 + \mathrm{CH}^2 = \mathrm{CD}^2
\end{eqnarray}
であるから、
$$
\mathrm{AB}^4 + \mathrm{AD}^4 = \mathrm{BD}^2 \cdot \mathrm{CD}^2
$$
が得られる。
補足
具体的に $\mathrm{AB}=p,\mathrm{AD}=q$ を求めるのは煩雑で、
$$
(p,q)=\left(\frac{\sqrt{6}}{4}\left(\sqrt{47+17\sqrt2}\pm\sqrt{47-17\sqrt2} \right),\frac{\sqrt{6}}{4}\left(\sqrt{47+17\sqrt2}\mp\sqrt{47-17\sqrt2} \right) \right)
$$
(複合同順) となります。
おすすめ問題
この問題を解いた人はこんな問題も解いています