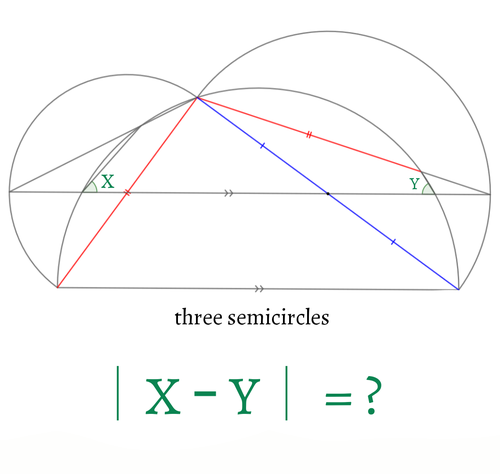
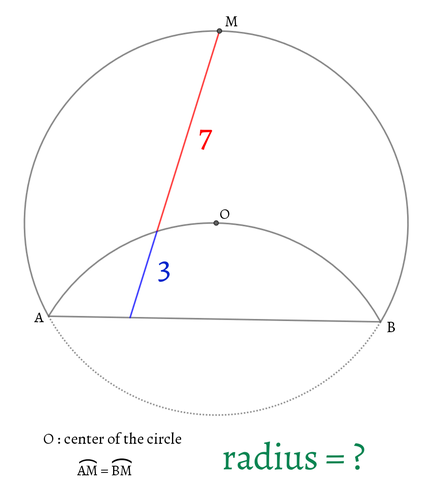
内接六角形がつくる角

tb_lb 自動ジャッジ 難易度: 数学 > 中学数学
2021年3月21日22:29 正解数: 9 / 解答数: 14 (正答率: 64.3%) ギブアップ不可
初等幾何 角度
ツイートする
問題
解答一覧
全解答 自分の解答
質問(0)

【補助線主体の図形問題 #007】
　今回は図形問題の王道から円がらみの求角問題を用意しました。手慣れている方なら脳内で処理できるくらいの計算量です。どうぞ円と角度の世界を堪能してください。

解答形式

${
\renewcommand\deg{{}^{\circ}}
\def\myang#1{\angle \mathrm{#1}}
\def\myarc#1#2{\stackrel{\style{transform:matrix(#1,0,0,1.5,0,2)}{\frown}}{\mathrm{#2}}}
}$　解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。角度は弧度法ではなく度数法で表すものとします。
（例） $12\deg$ → $\color{blue}{12.00}$　　$\frac{360}{7}^{\circ}$ → $\color{blue}{51.43}$
　入力を一意に定めるための処置です。
　近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。

ヒント内容の予告

  1. 全体方針をぼんやりと
  2. ある定理の紹介
  3. ヒント1・2の内容をやや具体的に
ヒント1

円周上には6つの点があり、6つの弧で構成されていますが、それぞれの弧に対する円周角が求まるわけではありません。ここでは弧2ヶ所分や3ヶ所分の円周角の和が求まったりします。それぞれの弧に対する円周角を文字で置き、その関係式を導いてみましょう。

ヒント2

円に対して交わらない2本の弦があって、それを延長してできる角の大きさは、特定の円周角の差で表せることが知られています。「アルハゼンの定理」でウェブ検索してみるとこの内容が具体的にわかるかもしれません。

ヒント3

たとえば、$\myang{P}$の大きさは$\myarc{4.5}{AFED}$に対する円周角から$\myarc{2.3}{BC}$に対する円周角を引いた値と等しくなります。$\myang{Q}$、$\myang{R}$についても同様の式を導き、ひとまずは$\myarc{3.5}{BAF}$に対する円周角の大きさを目標としましょう。

スポンサーリンク

解答提出

この問題は自動ジャッジの問題です。 解答形式が指定されていればそれにしたがって解答してください。

Discordでログイン Sign in with Google パスワードでログイン

ログインすると？ ログインすると、解答・ギブアップをする他に、問題を投稿したり、ランキングで競うことができます。

または

おすすめ問題

この問題を解いた人はこんな問題も解いています

22月前

7

問題文

図の条件の下で、赤で示した線分の長さ $x$ を求めてください。

解答形式

$x^2$ の値を半角数字で解答してください。

21月前

10

問題文

図の条件の下で、青で示した三角形の面積を求めてください。

解答形式

解答は互いに素な正整数 $a,b$ を用いて $\dfrac{a}{b}$ と表せるので、$a+b$ の値を半角数字で解答してください。

17月前

6

問題文

図の条件の下で，線分 $AB$ の長さを求めてください．
※orthocenter：垂心，circumcenter：外心

解答形式

$AB^2$ の値は互いに素な正整数 $a,b$ を用いて $\dfrac{a}{b}$ と表せるので，$a+b$ の値を解答してください．

求長問題26

Kinmokusei 自動ジャッジ 難易度:
2年前

6

問題文

直角二等辺三角形と、その頂角を通る円が図のように配置されています。青で示した線分の長さを求めてください。

解答形式

半角数字で解答してください。

問題❹

rakuraku1216 自動ジャッジ 難易度:
14月前

10

4×4の16マスがある。このマス目を赤、青、黄、緑で塗ることを考える。

A：縦と横のどの辺をとっても赤、青、黄、緑が一回ずつ出現する。
B：以下のように4つの部屋に分割したときにどの部屋をとっても赤、青、黄、緑が1回ずつ出現する。
□□｜□□
□□｜□□
＿＿｜＿＿
□□｜□□
□□｜□□

AとBを両方満たす塗り方は何通りありますか？
（例：30通りだったら、30と答えなさい）

23月前

11

問題文

図の条件の下で、緑の線分の長さ $x$ を求めてください。

解答形式

$x^2$ の値を半角数字で解答してください。

求長問題

Kinmokusei 自動ジャッジ 難易度:
3年前

23

問題文

円の一部を折り返した図形です。赤、青の線分の長さがそれぞれ
7,3のとき、円の半径を求めてください。(解答形式に注意!)
折り返した円弧部分は元の円の中心を通ります。
Mは弧ABの中点です。
2020/07/04/13:29 解答に誤りがあったため更新しました。

解答形式

$自然数A,B,Cを用いてradius=\frac{A\sqrt{B}}{C} と表せます。
A+B+Cを解答してください。$
$A,Cは既約分数の形に、Bは根号の中が最小となるようにしてください。$
$例: \frac{4\sqrt{18}}{6}=2\sqrt{2}→A=2,B=2,C=1→5と解答$

2年前

10

【補助線主体の図形問題 #025】
　このところ円がらみの出題が続いていたので、今回は直線図形だけで固めてみました。暗算でさくっと解いてしまってください！

解答形式

${
\def\cm{\thinspace \mathrm{cm}}
\def\mytri#1{\triangle \mathrm{#1}}
}$　解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。
（例） $12\cm^2$ → $\color{blue}{12.00}$　　$10\sqrt{2}\cm^2$ → $\color{blue}{14.14}$　　$\dfrac{1+\sqrt{5}}{2} \cm^2$ → $\color{blue}{1.62}$
　入力を一意に定めるための処置です。
　たとえば答えに無理数を含む場合、$\sqrt{2}=1.41$や$\pi=3.14$などでは必要な桁が足りない場合があるのでご注意ください。
　近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。

ヒント内容の予告

  1. 注目点をぼんやりと
  2. ヒント1の続き
  3. ヒント2の続き

直角三角形と8個の円

tb_lb 自動ジャッジ 難易度:
3年前

10

【補助線主体の図形問題 #006】
　投稿日である今日3月14日は、円周率$\pi$の近似値 $3.14$ になぞらえて「円周率の日」と定められています。ということで「円周率の日」記念に円多めの問題を用意しました。
　補助線が活躍するのはいつも通りです。ちょっとした知識があると暗算で処理可能ですが、そうでなくとも大した計算量ではありません。どうぞ円まみれのお時間を楽しんでいただければ幸いです。

解答形式

${
\def\cm{\thinspace \mathrm{cm}}
\def\mytri#1{\triangle \mathrm{#1}}
}$　解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。
（例） $12\cm^2$ → $\color{blue}{12.00}$　　$10\sqrt{2}\cm^2$ → $\color{blue}{14.14}$　　$\dfrac{1+\sqrt{5}}{2} \cm^2$ → $\color{blue}{1.62}$
　入力を一意に定めるための処置です。
　たとえば答えに無理数を含む場合、$\sqrt{2}=1.41$や$\pi=3.14$などでは必要な桁が足りない場合があるのでご注意ください。
　近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。

ヒント内容の予告

  1. 全体の方針をぼんやりと
  2. ヒント1の内容をやや具体的に
  3. ヒント2の続き

求面積問題29

Kinmokusei 自動ジャッジ 難易度:
2年前

8

問題文

図の条件のもとで、緑の正三角形の面積を求めてください。

※ hexagram : 六芒星

解答形式

半角数字で回答してください。

2年前

9

【補助線主体の図形問題 #017】
　今回は方針により計算量が変化する問題を用意しました。とはいえ暗算で解くには幾分厳しいです。簡単な計算用紙＆筆記具をお手元にご用意の上で挑戦してみてください。

解答形式

${
\def\cm{\thinspace \mathrm{cm}}
\def\mytri#1{\triangle \mathrm{#1}}
}$　解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。
（例） $12\cm$ → $\color{blue}{12.00}$　　$10\sqrt{2}\cm$ → $\color{blue}{14.14}$　　$\dfrac{1+\sqrt{5}}{2} \cm$ → $\color{blue}{1.62}$
　入力を一意に定めるための処置です。
　たとえば答えに無理数を含む場合、$\sqrt{2}=1.41$や$\pi=3.14$などでは必要な桁が足りない場合があるのでご注意ください。
　近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。

ヒント内容の予告

  1. 全体方針をぼんやりと
  2. ヒント1の続き
  3. ヒント2の続き
  4. ヒント3の続き

求面積問題15

Kinmokusei 自動ジャッジ 難易度:
3年前

10

問題文

緑色の五角形の面積を求めてください。
紫でしめした3つの角は等しく、赤同士、青同士の線分はそれぞれ等しい長さです。

解答形式

半角数字で解答してください。