問題文
実数 $a,b,c$ が $a^2+b^2+c^2\leqq 1$ を満たして動くとき、
座標空間上の点 $(a+b+c, ab+bc+ca, abc)$ が動く領域を $D$ とする。
以下の問いに答えよ。
⑴ $yz$ 平面に平行な平面 $\pi_t\colon \ x=t$ と $D$ が共有点を持つような実数 $t$ の範囲を求めよ。
⑵ $t$ が⑴で求めた範囲にあるとき、平面 $\pi_t$ と $D$ の共通部分を $E_t$ とする。
このとき、 ある $t$ の関数 $m(t), M(t)$ および $t$ と $y$ の関数 $p(t,y),q(t,y)$ が存在して、
$$
\begin{eqnarray}
E^1_t &=& \{ (x,y,z)|\ x=t,\ m(t) \leqq y \leqq M(t) \}\\
E^2_t &=& \{ (x,y,z)|\ x=t,\ z^2+p(t,y)z+q(t,y)\leqq0 \}
\end{eqnarray}
$$
とおけば $E_t = E^1_t \cap E^2_t $ と表せる。このような $m(t), M(t), p(t,y),q(t,y)$ を求めよ。
⑶ $E_t$ の面積を $S(t)$ とおく。$t$ が⑴で求めた範囲にあるとき、$S(t)$ を $t$ の式で表せ。 ただし、 $E_t$ がただ一点からなるときは $S(t)=0$ であるとする。
⑷ $D$ の体積 $V$ を求めよ。
解答形式
⑷のみ解答せよ。解は $V = \frac{\sqrt{(ア)}}{(イウ)}\pi$ と書ける。(ア)、(イウ)に当てはまる自然数をそれぞれ1,2行目に半角で入力せよ。ここでア,イ,ウの各文字には0から9までの整数のいずれかが入る。たとえば(ア)=3(イウ)=57 と解答する場合は、1行目に「3」、2行目に「57」と入力せよ。なお、根号の中身が最小になるように解答すること。
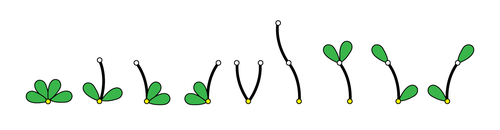 ここで,ある点に着目したときに,その点から出ている葉と枝の並びが異なるものは区別することに注意しましょう。
ここで,ある点に着目したときに,その点から出ている葉と枝の並びが異なるものは区別することに注意しましょう。