問題
以下の問に関して, $2.71<e<2.72$ , $3.14<π<3.15$ とする.
(1) $a≠0$ のとき $a+1$ , $e^a$ の大小を比較せよ.
(2) $α>0$ かつ $β>0$ かつ $α≠β$ のとき,
$\hspace{11pt} $ $α-β$ , $β(logα-logβ)$ の大小を比較せよ.
(3) $e^π$ , $π^e$ の大小を比較せよ.
(4) $e^{e^e},e^{e^π},e^{π^e},e^{π^π},π^{e^e},π^{e^π},π^{π^e},π^{π^π} $ の大小を比較せよ.
$\hspace{11pt} $ここで, $a^{b^c}$は $a^{(b^c)} $を表す.
解答形式
(1) ① $a+1$ ② $e^a$
(2) ① $α-β$ $\:$② $β(logα-logβ)$
(3) ① $e^π$ ② $π^e$
(4) ①$e^{e^e}$②$e^{e^π}$③$e^{π^e}$④$e^{π^π}$⑤$π^{e^e}$⑥$π^{e^π}$⑦$π^{π^e}$⑧$π^{π^π} $
として問ごとに改行し,小さい順に左から半角数字を用いて並べよ.
(例)12345678
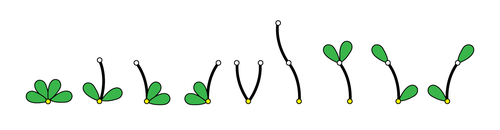 ここで,ある点に着目したときに,その点から出ている葉と枝の並びが異なるものは区別することに注意しましょう。
ここで,ある点に着目したときに,その点から出ている葉と枝の並びが異なるものは区別することに注意しましょう。