数学の問題一覧
公開日時: 2023年10月30日14:07 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
代数
問題文
実数 $x,y$ が $x^2+y^2 = 1$ を満たしています. このとき, $\cfrac{7xy-5x-5y+22}{x^2-10x+25}$ のとり得る最大値を $M$, 最小値を $N$ としたときの $NM$ の値を求めてください. ただし, 答えは互いに素な正整数 $a,b$ を用いて $\cfrac{b}{a}$ と表されるので, $a+b$ の値を解答して下さい.
解答形式
非負整数値を解答して下さい.
公開日時: 2022年1月16日3:36 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
2つの正三角形が図のように配置されています。青で示した3つの線分の長さの和($x+y+z$ の値)を求めてください。

解答形式
$(x+y+z)^2$ は正整数になるので、この値を半角数字で解答してください。
公開日時: 2023年5月7日22:28 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
初等幾何 面積

【補助線主体の図形問題 #096】
1週出題を休んでしまいましたが、今週の図形問題です。今回は重めの面積関係の問題となりました。たっぷりと補助線を引きながら、存分に楽しんでもらえたら幸いです。
解答形式
${\def\cm{\thinspace \mathrm{cm}}}$ 解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。
(例) $12\cm^2$ → $\color{blue}{12.00}$ $10\sqrt{2}\cm^2$ → $\color{blue}{14.14}$ $\dfrac{1+\sqrt{5}}{2} \cm^2$ → $\color{blue}{1.62}$
入力を一意に定めるための処置です。
たとえば答えに無理数を含む場合、$\sqrt{2}=1.41$や$\pi=3.14$などでは必要な桁が足りない場合があるのでご注意ください。
近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。
公開日時: 2022年1月2日22:37 / ジャンル: 数学 / カテゴリ: 算数 / 難易度: / ジャッジ形式: 自動ジャッジ
パズル 西暦問題 虫食算 2022年問題
${}$ 西暦2022年問題第2弾です。第1弾に引き続き虫食算で、今回は割り算にしてみました。数学的手法(約数や倍数、偶奇性や剰余、不等式による絞り込み、などなど)を適宜用いることで面倒な場合分けや仮置きを軽減できるよう仕込んでいるのは変わりません。パズル的に解くのもよし、数学的にゴリゴリ解くのもよし、どうぞお好きなようにお楽しみください!
解答形式
${}$ 解答は2行目を「被除数÷除数」の形で入力してください。
(例) $2022 \div 102 = 19$ 余り $84$ → $\color{blue}{2022 \text{÷} 102}$
入力を一意に定めるための処置です。数字は半角で、「÷」の演算記号はTeX記法(\div)ではなく全角記号の「÷」でお願いします。
公開日時: 2020年10月30日20:00 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
(1)$p$を奇素数とし、$\frac{1}{p}$を2進数で表示したときの循環節(※)が2以上8以下であるような$p$は6つ存在する。フェルマーの小定理を用いて$p$とその$p$に対する$\frac{1}{p}$の循環節の長さの関係を導き、6つの$p$の値を全て答えよ。
(2)$p$を奇素数とし、$\frac{1}{p}$を2進数で表示したときに最大で1が連続して並ぶ個数を$f(p)$とおく。例えば$\frac{1}{3}=0.01010…_{(2)}$より$f(3)=1$である。(1)を満たす$p$の中で$f(p)$が最大となるのは$p$がいくらのときか。Midyの定理を用いることによって求め、その値を答えよ。
(※)循環節とは、循環小数の繰り返される数字の列のうちその長さが最小でありかつその先頭が最も先に来るようなもののことである。例えば$\frac{1}{3}=0.01010…_{(2)}$となり、このときの循環節は$01$であり、$0101$や$10$は循環節とならない。
解答形式
(1)の全ての答えを小さい順に1~6行目に半角数字で入力してください。また、(2)の答えを7行目に半角数字で入力してください。
公開日時: 2021年12月19日23:44 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
初等幾何 長さ

【補助線主体の図形問題 #040】
2021年も残り半月を切りました。慌ただしい頃合いかもしれませんが、ちょいと一息図形問題などいかがでしょうか。
適当に補助線を引いても気づいたら解けてしまうような問題かもしれません。腕に覚えのある方はぜひ完全に脳内で処理し切ってみてください。
解答形式
${\def\cm{\thinspace \mathrm{cm}}}$ 解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。
(例) $12\cm$ → $\color{blue}{12.00}$ $10\sqrt{2}\cm$ → $\color{blue}{14.14}$ $\dfrac{1+\sqrt{5}}{2} \cm$ → $\color{blue}{1.62}$
入力を一意に定めるための処置です。
たとえば答えに無理数を含む場合、$\sqrt{2}=1.41$や$\pi=3.14$などでは必要な桁が足りない場合があるのでご注意ください。
近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。
公開日時: 2021年12月12日10:36 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
正三角形・長方形・半円を組み合わせた以下の図形について、図中緑の線分の長さが6のとき、図形全体の面積を求めてください。

解答形式
半角数字で解答してください。
公開日時: 2024年3月7日19:00 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
正三角形 $ABC$ において,その外接円の劣弧 $BC$ 上(端点を除く)に点 $D$ をとり,三角形 $ABD,BCD,CAD$ の内心をそれぞれ $I_C,I_A,I_B$ とすると,$I_BI_C=2I_AI_B=6$ が成立しました.このとき,$BC$ の長さの $2$ 乗を求めてください.
解答形式
答えは正整数値になるので,半角で解答してください.
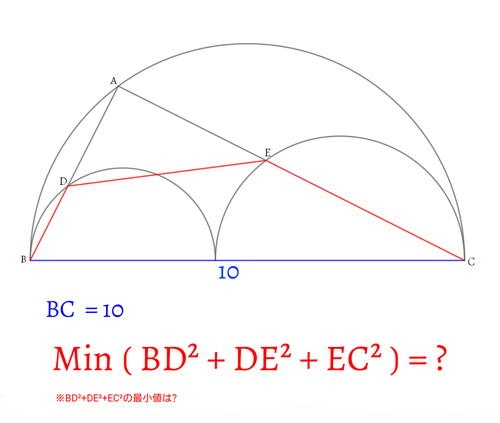
公開日時: 2020年7月25日21:03 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
直径10の半円中に、直径の和が10となる2つの半円を図のように配置します。点Aを大半円の弧上にとり、線分AB,ACと小半円の交点をD,Eとします。
$BD^2+DE^2+EC^2$が最小となるようにしたとき、その最小値を求めてください。
解答形式
半角数字で解答してください。
公開日時: 2024年1月6日21:28 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
整数問題 西暦問題 2024年問題
${}$ 西暦2024年問題第6弾です。いよいよ整数問題のお出ましとなりました。ある程度は手を動かす必要がありますが、あることに気づけば調べる候補をぐっと減らすことができます。約数の個数を求めるのが面倒な方はWolfram|Alpha https://www.wolframalpha.com なども併用して構いません。
解答形式
${}$ 解答は求める$n$の最小値をそのまま入力してください。
(例)$n=2106$ → $\color{blue}{2106}$
公開日時: 2021年11月7日22:29 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
初等幾何 角度

【補助線主体の図形問題 #035】
11月に入りました。11月11日に先んじて11だらけの図形問題をお送りします。補助線しだいで処理量は大きく変わりますが、暗算可能な解法も存在します。補助線の威力を存分にお楽しみください!
解答形式
${\renewcommand\deg{{}^{\circ}}}$ 解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。角度は弧度法ではなく度数法で表すものとします。
(例) $12\deg$ → $\color{blue}{12.00}$ $\frac{360}{7}^{\circ}$ → $\color{blue}{51.43}$
入力を一意に定めるための処置です。
近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。
公開日時: 2020年10月7日23:53 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
2曲線
$
\begin{cases}
y=2x^3+10x^2+12x+7 \newline
y=x^2+5x+13
\end{cases}
$
で囲まれる部分の面積$S$を求めよ。
解答形式
答えは
$\displaystyle\frac{[abc]}{[de]}$
という形になります。($a,b,c,d,e$は1桁の自然数)
センター、共通テスト方式で答えてください。
例:
$S=\displaystyle\frac{765}{13}$のときは「76513」と入力する。

