問題文
円の一部を折り返した図形です。赤、青の線分の長さがそれぞれ
7,3のとき、円の半径を求めてください。(解答形式に注意!)
折り返した円弧部分は元の円の中心を通ります。
Mは弧ABの中点です。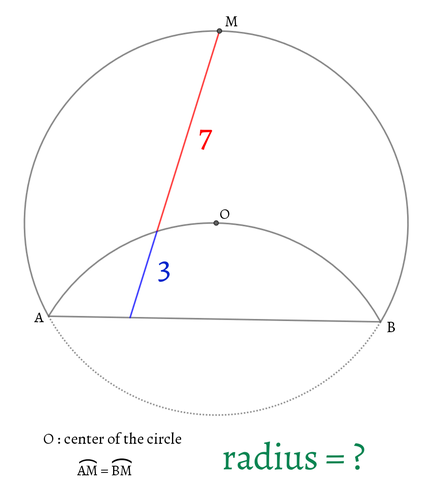
2020/07/04/13:29 解答に誤りがあったため更新しました。
解答形式
$自然数A,B,Cを用いてradius=\frac{A\sqrt{B}}{C} と表せます。
A+B+Cを解答してください。$
$A,Cは既約分数の形に、Bは根号の中が最小となるようにしてください。$
$例: \frac{4\sqrt{18}}{6}=2\sqrt{2}→A=2,B=2,C=1→5と解答$
ヒント1
方べきの定理を使います。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています