問題文
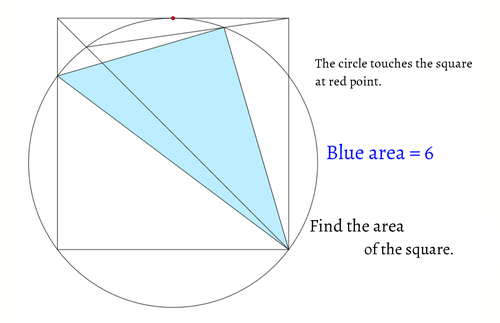
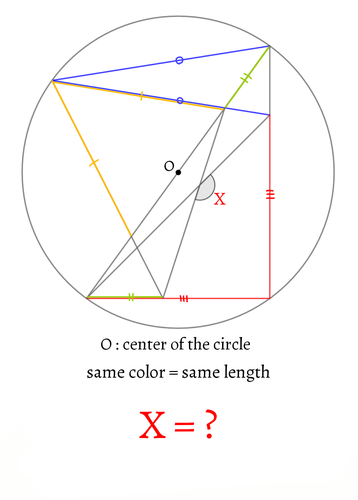
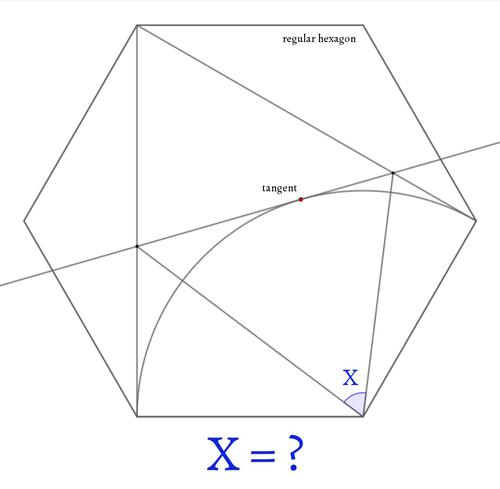
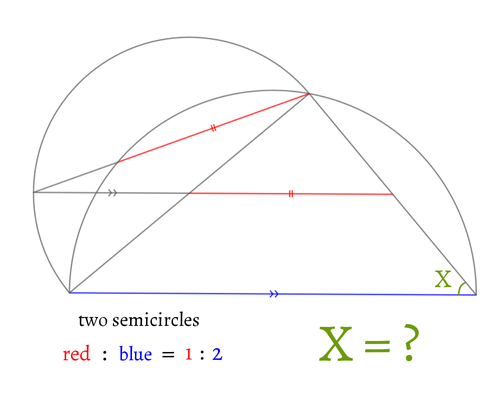
半円2つが図のように配置されています。
赤い線分と青い線分は長さの比が1:2です。
このとき、Xの角度を求めてください。
解答形式
半角数字で入力してください。
「度」や「°」は付けないでください。
例:X=57° → 57
ヒント1
正三角形を見つけましょう。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています