この問題はコンテスト「KOH Mathematical Contest #1」の問題です。
問題文
$x=0$ で微分可能な実数値連続関数 $f(x),g(x)$ は任意の実数 $x,y$ に対して以下の式を満たすとする。以下の空欄を埋めよ。
$$
f(x+y)=f(x)g(y)+g(x)f(y)\\g(x+y)=g(x)g(y)-f(x)f(y)
$$
$f'(0)=2,g'(0)=1$ であるとする。今 $f(0)=\fbox{ア},g(0)=\fbox{イ}$ であるので
$$
\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}=\fbox{ウ}f(x)+\fbox{エ}g(x)\\\lim_{h\to 0}\frac{g(x+h)-g(x)}{h}=\fbox{オ}f(x)+\fbox{カ}g(x)
$$
となる。 $h(x)=(f(x))^2+(g(x))^2$ とおくと
$$
h'(x)=\fbox{キ}h(x)
$$
これより
$$
\dfrac{d}{dx}(h(x)e^{-\fbox{キ}x})=\fbox{ク}
$$
がわかるので、
$$
h(x)=\fbox{ケ}e^{\fbox{コ}x}
$$
を得る。
解答形式
半角数字で改行区切りで記述せよ。たとえば $\fbox{ア}$ に $100$ , $\fbox{イ}$ に $-99$ と答えたい場合には1行目に $100$ , 2行目に $-99$ を記述せよ。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています
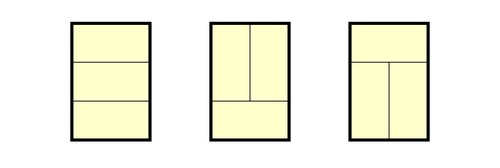 の $3$ 通りだから $a_1=3$ である。このとき
の $3$ 通りだから $a_1=3$ である。このとき