連立する整数問題

問題文

$m$ と $n$ を互いに素な自然数とします．実数係数多項式 $f(x)$ が次の性質をもっているとき，$f(x)$ を $m,n$-生成の多項式と呼ぶことにします．

• 性質：すべての実数係数多項式 $g(x)$に対して，$f(x)g(x)=h(x^m, x^n)$ となるような実数係数の2変数多項式 $h(x,y)$ が存在する．

$x^k$ がすべての $10,n$-生成の多項式を割り切るような最大の自然数 $k$ は

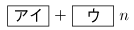
です．ただし，単項式も多項式に含まれるとします．

解答形式

センター試験方式です．ア，イ，ウにはそれぞれ 0,1,2,3,4,5,6,7,8,9 および -,a,b,c,d のいずれか1文字が当てはまります．ア，イ，ウに 1, 2, 3 が当てはまるなら，123 と回答してください．

問題文

$x^4+y^4+z^4+w^4+(x^2+y^2+z^2+w^2)(xy+xz+xw+yz+yw+zw)+4xyzw$
を因数分解せよ。

解答形式

TeXで入力してください。項の順番に関しては辞書式順で入力してください。字数の高い因数を先に書いてください。
例1:
$(x^2+y^2+z^2+w^2)(x+y+z+w)$と答えるには
(x^2+y^2+z^2+w^2)(x+y+z+w)を入力してください。
例2:
$x,y,z,w$から重複せず3文字を選び、かけ合わせた項4つを辞書式順に並べると
$xyz,xyw,xzw,yzw$

問題文

$x,y$を自然数とする。$x^2+8y$と$y^2+8x$がともに平方数になるような$x,y$の組$(x,y)$をすべて求めよ。

解答形式

例えば、$(x,y)=(1,2),(13,4),(51,16)$と答えたい場合は

12
134
5116

と入力してください。解の組は$x$の値が小さい順に並べてください。$x$の値が同じで$y$の値が異なる場合は$y$の値が小さい方を先に入力してください。

問題文

一次関数$f(x)$と$g(x)$は以下を満たす
(但し$t$は定数)
$$
\begin{cases} f(x)=4x+g(t)\\
g(x)=−2x-f(t) \end{cases}
$$
$f(2)=2$のとき、$g(2)$の値を求めよ。

解答形式

自由

問題文

≪aは定数とする。xの関数f(x)に対しf(a)とは、f(x)にx=aを代入した値である。例えば、f(x)=2xが与えられれば、f(2)の値は4となる≫

f(x)=3x−1についてf(a+1)をaを用いて表せ

問題文

どの辺の長さも整数である$\triangle ABC$の面積を$S$とする。$S^2$の小数部分を求めよ。

解答形式

とりうるすべての小数部分を小さい順に都度改行、列挙してください。
例：
「0,1/2,1/3,1/6,1/√5」の場合、

0
0.5
0.'3'
0.1'6'
1/\sqrt{5}

問題文

行列$A$を次で定義する。
$$
A=
\begin{pmatrix}
6& -3 & -7 & 0 & 0 & 0\\
-1 & 2 & 1 & 0 & 0 & 0\\
5& -3 & -6 & 0 & 0 & 0\\
0& 0 & 0 & 1 & 2 & 1\\
0& 0 & 0 & -1 & 4 & 1\\
0& 0 & 0 & 2 & -4 & 0\\
\end{pmatrix}
$$
このとき次の実線形空間の次元を求めよ。
$$
V=\{X\in M_{6}(\mathbb{R})\mid AX=XA\}
$$
ただし、$M_{6}(\mathbb{R})$とは6行6列の実正方行列全体の集合である。

解答形式

半角数字で答えよ。

問題文

漸化式
$$
a_{n+3}=3a_{n+2}-4a_{n+1}+2a_n\quad (n=1,2,\cdots)
$$および
$$
a_1=1, \; a_2=0, \; a_3=0
$$を満たす数列 $\{a_n\}$ を考える。次の空欄 $\fbox{ア}$ 〜 $\fbox{フ}$ に当てはまる数字を答えなさい。

• 漸化式
  $$
  a_{n+3}=3a_{n+2}-4a_{n+1}+2a_n\quad (n=1,2,\cdots)
  $$を満たす数列全体の集合を $V$ とする。数列 $a_n, b_n\in V$ および $c\in\mathbb{C}$ に対して，第 $n$ 項が $ca_n, a_n+b_n$ であるような数列をそれぞれ数列 $a_n$ の $c$ 倍，数列 $a_n, b_n$ の和と定義することにすると，この和とスカラー倍により $V$ は $\mathbb{C}$ 上のベクトル空間になる（確かめよ）。ここで，$V$ の元 $a_n$ は，$a_1, a_2, a_3$ を定めることで完全に決定できる。すなわち，写像 $\varphi: V \to \mathbb{C}^3$ を
  $$
  \varphi(a_n)=\begin{pmatrix} a_1 \\ a_2 \\ a_3\end{pmatrix}
  $$で定めると，$\varphi$ は全単射である。しかも，$\varphi$ は線型写像だから，$\varphi$ はベクトル空間の同型になる。$V$ は $\fbox{ア}$ 次元である。また，$e_n^{(1)}, e_n^{(2)}, e_n^{(3)}\in V$ を
  $$
  \varphi(e_n^{(1)})=\begin{pmatrix} 1 \\ 0 \\ 0\end{pmatrix},\; \varphi(e_n^{(2)})=\begin{pmatrix} 0 \\ 1 \\ 0\end{pmatrix},\; \varphi(e_n^{(3)})=\begin{pmatrix} 0 \\ 0 \\ 1\end{pmatrix}
  $$となるように定めると，$e_n^{(1)}, e_n^{(2)}, e_n^{(3)}$ は $V$ の基底になる。

• $V$ 上の線型変換 $L: V\to V$ を次のように定義する。$a_n\in V$ に対して，$L(a_n)$ を第 $1, 2, 3$ 項がそれぞれ $a_2, a_3, a_4$ である数列とする（$L$ が線型写像になることを確かめよ）。このとき，$L(a_n)$ の第 $n$ 項は $a_{n+\fbox{イ}}$ である。基底 $e_n^{(1)}, e_n^{(2)}, e_n^{(3)}$ のもとでの $L$ の表現行列 $L_A$ は
  $$
  L_A=\begin{pmatrix} \fbox{ウ} & \fbox{エ} & * \\ \fbox{オ} & \fbox{カ} & \fbox{キ} \\ \fbox{ク} & \fbox{ケコ} & \fbox{サ}\end{pmatrix}
  $$である。

• $L_A$ の固有値を $\lambda^{(1)}, \lambda^{(2)}, \lambda^{(3)}$ とする（$\lambda^{(1)}\in\mathbb{R}, {\rm Im}(\lambda^{(2)})>0, {\rm Im}(\lambda^{(3)})<0$）。このとき
  \begin{align}
  \lambda^{(1)}&=\fbox{シ}\\
  {\rm Re}(\lambda^{(2)})={\rm Re}(\lambda^{(3)})&=\fbox{ス}\\
  {\rm Im}(\lambda^{(2)})=-{\rm Im}(\lambda^{(3)})&=\fbox{セ}
  \end{align}である。

• 固有値 $\lambda^{(1)}, \lambda^{(2)}, \lambda^{(3)}$ に対応する固有ベクトルをそれぞれ $\alpha^{(1)}, \alpha^{(2)}, \alpha^{(3)}$ とする。固有ベクトルには定数倍の不定性があるが，$\alpha^{(j)}\;(j=1,2,3)$ の第 $1$ 成分が固有値 $\lambda^{(j)}$ に一致するようにとると
  \begin{align}
  \alpha^{(1)}=\begin{pmatrix} \lambda^{(1)} \\ \fbox{ソ} \\ * \end{pmatrix},\; \alpha^{(2)}=\begin{pmatrix} \lambda^{(2)} \\ \fbox{タ}\;i \\ * \end{pmatrix},\; \alpha^{(3)}=\begin{pmatrix} \lambda^{(3)} \\ * \\ \fbox{チツ}-\fbox{テ}\;i \end{pmatrix}
  \end{align}である。

• $\varphi(\beta_n^{(1)})=\alpha^{(1)}, \;\varphi(\beta_n^{(2)})=\alpha^{(2)}, \;\varphi(\beta_n^{(3)})=\alpha^{(3)}$ となる数列 $\beta_n^{(1)}, \beta_n^{(2)}, \beta_n^{(3)}\in V$ をとる。$\beta_n^{(1)}, \beta_n^{(2)}, \beta_n^{(3)}\in V$ は $V$ の基底をなすから，$V$ の任意の元 $a_n$ はこれらの線型結合で表すことができる。例えば，$a_n\in V$ が
  $$
  a_1=1, \; a_2=0, \; a_3=0
  $$を満たすとき
  $$
  a_n=\fbox{ト}\;\beta_n^{(1)}-\frac{\beta_n^{(2)}-\beta_n^{(3)}}{\fbox{ナ}\; i}
  $$が成り立つ。これを変形すると
  $$
  a_n=\fbox{ニ}-\left(\sqrt{\fbox{ヌ}}\;\right)^n\sin\left(\frac{n\pi}{\fbox{ネ}}\right)
  $$となる。また，$a_1,\cdots, a_{100}$ のうち $a_n$ が最大となるのは $n=\fbox{ノハ}, \fbox{ヒフ}$ のときである。ただし $\fbox{ノハ} < \fbox{ヒフ}$ とする。

※この問題では，数列とは写像 $a: \mathbb{N} \to \mathbb{C}$ のことをいう。$n\in\mathbb{N}$ に対して，$a(n)$ のことを単に $a_n$ と表記する。また，記号の濫用であるが $a$ を $\{a_n\}, a_n$とも書く。

解答形式

空欄 $\fbox{ア}$ 〜 $\fbox{フ}$ には，半角数字 0 - 9 または記号 - のいずれかが当てはまります。$\fbox{ア}$ 〜 $\fbox{フ}$ に当てはまるものを改行区切りで入力してください。

【補助線主体の図形問題 #001】
　2013年よりツイッターなどで補助線主体の初等幾何の問題を披露してきたtb_lbと申します。このたびこの「ポロロッカ」を知り、今まで作ってきた問題を再発表することを決めました。気まぐれに投稿してまいりますので、見かけた際にはどうぞよろしくお願いします。
　さて、ご挨拶代わりの1問目は易しめに抑えてみました。答えを出すだけなら代数的な処理で十分ですが、いささか面倒です。適切な補助線を引くと面倒な計算を避けることができますので、ぜひ補助線解法を考えてみてください。

解答形式

${\def\cm{\thinspace \mathrm{cm}}}$　解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。
（例） $12\cm^2$ → $\color{blue}{12.00}$　　$10\sqrt{2}\cm^2$ → $\color{blue}{14.14}$　　$\dfrac{1+\sqrt{5}}{2} \cm^2$ → $\color{blue}{1.62}$
　入力を一意に定めるための処置です。
　たとえば答えに無理数を含む場合、$\sqrt{2}=1.41$や$\pi=3.14$などでは必要な桁が足りない場合があるのでご注意ください。
　近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。

ヒント内容の予告

1. 大雑把な方針の選択肢
2. ヒント1の続き
3. 補助線の方針
4. 上記のヒントを無視して強引な解法をとるなら

問題文

図のように長方形や直角三角形の内接円が配置されています。青で示した角の角度を求めてください。

解答形式

度数法で求め、半角数字で0以上360未満の整数を解答してください。
※度や°などの単位は付けないでください。

問題文

（2020.9.26 11:57追記）
解答形式に不備があったため、訂正致しました。

図の青、緑、赤の線分の長さを$X,Y,Z$、斜線部の面積を$S$とすると、次の式が成り立つ。
$$
\frac{[ア]}{S}=\frac{[イ]}{Z}\left(\frac{1}{X}+\frac{1}{Y}\right)
$$

なお、図の曲線は半円の弧である。

解答形式

$[ア],[イ]$にはともに自然数が入ります。その和を半角数字で解答してください。
ただし、その和が最小となるように解答してください。
例:$[ア]=4,[イ]=2$なら$6$ではなく(両辺を$2$で割ることにより)$3$と解答。

問題文

$△ABC$は鋭角三角形とします。次に、$A,B,C$から$BC,CA,AB$におろした垂線の足をそれぞれ$X,Y,Z$とし、$△ABC,△XYZ$の内接円の半径をそれぞれ$r,r'$とします。このとき、次の式の最小値を求めてください。
$$
\frac{r}{r'}\cos{\frac A2}\cos{\frac B2}\cos{\frac C2}
$$

解答形式

$$
\frac{r}{r'}\cos{\frac A2}\cos{\frac B2}\cos{\frac C2}\geq\frac{[ア]\sqrt{[イ]}}{[ウ]}=(最小値)
$$
となります。$[ア]+[イ]+[ウ]$を半角数字で解答してください。
ただし、$[ア],[イ],[ウ]$には自然数が入ります。また、分数部分は既約分数に、根号内の数字は最小となるようにしてください。