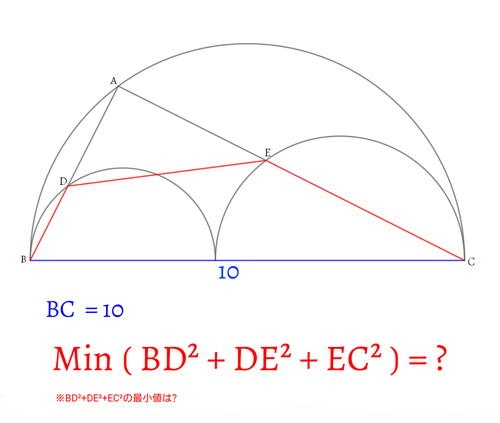
問題文
実数$ a $ を $a=\sqrt[3]{1+\sqrt2} +\sqrt[3]{1-\sqrt2}$ で定める。以下の問いに答えよ。
⑴ $a^3+3a-2=0$ であることを示せ。また、$0<a<2$ を示せ。
⑵ $x$ について以下の恒等式が成り立つことを示せ。
$$
x^4+4x-3=(x^2+a)^2-2a\left(x-\frac{1}{a}\right)^2
$$
⑶ 4次方程式 $x^4+4x-3=0$ の実数解を $a$ を用いて表せ。
解答形式
⑶のみ解答せよ。解は2つ存在し、
$$
x= -\sqrt{\frac{ア}{イ}}\ \pm \ \sqrt{\sqrt{\frac{ウ}{エ}}-\frac{オ}{カ}}
$$
の形である。ア~カのそれぞれには1から9までの自然数または文字$a$が入る。
ア~カに当てはまる数字または文字を、順にすべて半角で入力せよ。
たとえばア=2、イ=7、ウ=3、エ=5、オ=8、カ=$a$ と解答する場合は、
「27358a」と入力せよ。
ヒント1
$\alpha=\sqrt[3]{1+\sqrt2}, \beta=\sqrt[3]{1-\sqrt2}$ とおくと$\alpha^3+\beta^3 = 2, \alpha\beta=-1$ であることを用いよ。
また $f(t)=t^3+3t-2$ とおくと、$f(t)$が単調増加であることに注意せよ。
ヒント2
示すべき式の右辺を展開してみよ。⑴の結果を利用せよ。
ヒント3
⑵で示した式から、扱いやすい2つの方程式に帰着させよ。⑴で示した$a$を評価する不等式を用いて、2つの方程式のどちらが実数解を持つか吟味せよ。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています