hinu

問題

(1) $a,b$ を整数でない正の有理数とする。 $a^b$ は常に無理数か。

(2) $a$ を整数でない正の有理数とする。 $a^a$ は常に無理数か。

(3) $a,b$ を正の無理数とする。 $a^b$ は常に無理数か。

(4) $a$ を正の無理数とする。 $a^a$ は常に無理数か。

解答方法

解答欄に改行区切りで O (オー)または X (エックス)を記述せよ。正解判定は各行に対して行われ、完答のみ正解となる。

問題文

$\pi$ と $\dfrac{355}{113}$ はどちらが大きいか。ただし必要があれば積分

$$
\int_0^1\frac{x^8(1-x)^8(25+816x^2)}{3164(1+x^2)}dx
$$

を計算せよ。

解答形式

piまたは 355/113 で解答してください。

問題文

平面上に長方形 ${\rm ABCD}$ と点 ${\rm P}$ があり、 ${\rm AP}=11,{\rm BP}=9,{\rm CP}=3$ を満たしている。このとき ${\rm DP}$ の長さ $x$ を求めよ。

解答形式

半角数字で入力してください。

問題文

$a,b,c$ を実数とする。次の連立方程式を解け。

$$
a^2-4b-1=0\\
b^2-8c+28=0\\
c^2-6a+2=0\\
$$

解答形式

a,b,cを半角数字として(a,b,c)で解答してください。無理数などを使いたい場合はTeXコマンドを使用してください。

解答形式

半角数字とハイフン「-」で解答してください。

問題文

解答形式

「#」「%」「()」がそれぞれ「ある」「なし」のどちらであるかを、それぞれ一行目・二行目・三行目に答えてください。
それぞれの行は ある なし のいずれかで答えてください。

A君は $38\times 57$ を次のように計算した。

$$
\newcommand{\nc}{\newcommand}
\nc{\wake}[1]{\begin{cases} #1 \end{cases}}
\nc{\f}[2]{\dfrac{#1}{#2}}
\nc{\s}[1]{\{#1\}}
\nc{\pmat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\nc{\lr}[1]{\left( #1 \right)}
\nc{\com}[2]{{}_{#1}{\rm C}_{#2} \right)}
\nc{\bar}[1]{{\overline{#1}}}
\nc{\bb}[1]{{\mathbb {#1}}}
\nc{\rmn}[1]{{\rm #1}}
\nc{\q}{\quad}
\nc{\x}{\times}
\nc{\a}{\alpha}
\nc{\b}{\beta}
\nc{\th}{\theta}
\nc{\Q}[1]{\fbox{#1}}
\nc{\qq}{&\q\q\q\q\q&}\begin{eqnarray}38\qq 57 \qq \rm x\\19\qq 114\qq \rm o\\9\qq 228\qq \rm o\\4\qq 456\qq \rm x\\2\qq 912\qq \rm x\\1\qq \underline{1824}\qq \rm o\\ \qq 2166\qq \rm \\\end{eqnarray}
$$

A君の計算方法に基づいて以下の $43\x 71$ の計算の空欄を埋めよ。

$$
\nc{\qq}{&\q\q\q\q\q&}\begin{eqnarray}43\qq 71 \qq \rm o\\\Q{ア}\qq \Q{オ}\qq \rm \Q{ケ}\\\Q{イ}\qq \Q{カ}\qq \rm \Q{コ}\\\Q{ウ}\qq \Q{キ}\qq \rm \Q{サ}\\\Q{エ}\qq \Q{ク}\qq \rm \Q{シ}\\1\qq \underline{2272}\qq \rm o\\ \qq 3053\qq \rm \\\end{eqnarray}
$$

解答を改行区切りで入力せよ。ただし $\Q{ア}$ から $\Q{ク}$ には 1 から 9999 までの整数が入り、 $\Q{ケ}$ から $\Q{シ}$ には o または x が入る。

問題文

$$
\newcommand{\nc}{\newcommand}
\nc{\wake}[1]{\begin{cases} #1 \end{cases}}
\nc{\f}[2]{\dfrac{#1}{#2}}
\nc{\s}[1]{\{#1\}}
\nc{\pmat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\nc{\lr}[1]{\left( #1 \right)}
\nc{\com}[2]{{}_{#1}{\rm C}_{#2} \right)}
\nc{\bar}[1]{{\overline{#1}}}
\nc{\bb}[1]{{\mathbb {#1}}}
\nc{\rmn}[1]{{\rm #1}}
\nc{\q}{\quad}
\nc{\x}{\times}
\nc{\a}{\alpha}
\nc{\b}{\beta}
\nc{\th}{\theta}
\nc{\Q}[1]{\fbox{#1}}
$$

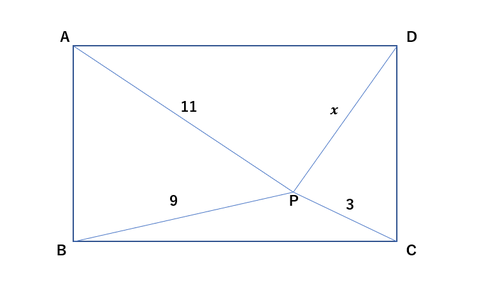
下のように $\rm AB=1\ ,\ BC=2$ の長方形 $\rm ABCD$ がある。点 $\rm P$ は $t=0$ で点 $\rm A$ におり、 $1$ 秒間に $1$ の速度で辺の上を進む。点 $\rm P$ が 点 $\rm A,B,C,D$ のいずれかにいるとき確率 $p$ で辺 $\rm AB$ に平行な向きに、 $1-p$ の確率で辺 $\rm AD$ に平行な向きに向きを変え、それ以外の場所で向きを変えることはないものとする。

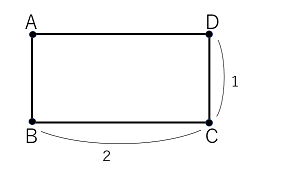
$p=\dfrac56$ とするとき点 $\rm P$ が $2n$ 秒後 $(n=0,1,2,\cdots)$ に点 $\rm A$ にいる確率を求めたい。

点 $\rm P$ が $2n$ 秒後に点 $\rm A,D$ にある確率を $A_n,D_n$ とおく。このとき $X_n=A_n+D_n$ とおくと漸化式
$$
X_{n+1}=\f{\Q{ア}}{\Q{イ}}X_n +\f{\Q{ウ}}{\Q{エ}}
$$
が成り立つ。また $Y_n=A_n-D_n$ とおくと漸化式
$$
Y_{n+2}-\f{\Q{オ}}{\Q{カ}}Y_{n+1}+\f{\Q{キ}}{\Q{ク}}Y_n=0
$$
が成り立つ。これらを初期条件 $X_0=\Q ケ\ ,Y_0=\Q{コ}\ ,Y_1=\f{\Q{サ}}{\Q{シ}}$ のもとで解くことで
$$
A_n=\f{\Q ス}{\Q セ}+\f{\Q ソ}{\Q タ}\lr{\f{\Q チ}{\Q ツ}}^n-\lr{\f{\Q テ}{\Q ト}}^n+\f{\Q ナ}{\Q ニ}\lr{\f{\Q ヌ}{\Q ネ}}^n
$$
を得る。なお ${\f{\Q チ}{\Q ツ}}<{\f{\Q ヌ}{\Q ネ}}$ である。

解答形式

上の空欄を埋めよ。解答は半角数字・改行区切りで入力すること。ただし $\Q ア$ から $\Q ネ$ にはそれぞれ 1 から 999 までの整数が入り、分数は既約分数の形で表してある。

問題文

$n\;(\geq 2)$ を自然数とするとき，以下の試行を行うことを考える。

試行

• $n$ 人が $0,1,2$ のいずれかひとつの数を無作為に選ぶ。
• 人 $i\; (i=1,2,\cdots, n)$ が選んだ数を $a_i$ とする。各人 $i$ に対して，
  $$
  a_i\equiv\sum_{j=1}^n a_j\; ({\rm mod} \; 3)
  $$ならば人 $i$ は生存し，そうでないなら脱落する。この試行をmodじゃんけんと呼ぶことにする。

$n$ 人がmodじゃんけんを $1$ 回行い，全員が生存するか全員が脱落するとき，modじゃんけんの結果はあいこになると定義する。

$n$ 人がmodじゃんけんを $1$ 回行ってあいこになる確率を $p_n$ とするとき

$$
p_2=\frac{\fbox{ア}}{\fbox{イ}},\; p_3=\frac{\fbox{ウ}}{\fbox{エ}},\; p_4=\frac{\fbox{オ}}{\fbox{カキ}}
$$

である。$n$ を $\fbox{ク}$ で割った余りが $\fbox{ケ}$ であるとき

$$
p_n=\frac{\fbox{コ}^{n}+\fbox{サ}}{\fbox{シ}^n}
$$

であり，そうでないときには

$$
p_n=\frac{\fbox{コ}^{n}+\fbox{ス}}{\fbox{シ}^n}
$$

である。また，

$$
\lim_{n\to\infty} p_n=\fbox{セ}
$$

が成り立つ。

解答形式

空欄 $\fbox{ア}$ 〜 $\fbox{セ}$ には，半角数字 0 - 9 または記号 - のいずれかが当てはまります。$\fbox{ア}$ 〜 $\fbox{セ}$ に当てはまるものを改行区切りで入力してください。分数はこれ以上約分できない形で解答してください。

問題文

$x=0$ で微分可能な実数値連続関数 $f(x),g(x)$ は任意の実数 $x,y$ に対して以下の式を満たすとする。以下の空欄を埋めよ。

$$
f(x+y)=f(x)g(y)+g(x)f(y)\\g(x+y)=g(x)g(y)-f(x)f(y)
$$

$f'(0)=2,g'(0)=1$ であるとする。今 $f(0)=\fbox{ア},g(0)=\fbox{イ}$ であるので

$$
\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}=\fbox{ウ}f(x)+\fbox{エ}g(x)\\\lim_{h\to 0}\frac{g(x+h)-g(x)}{h}=\fbox{オ}f(x)+\fbox{カ}g(x)
$$

となる。 $h(x)=(f(x))^2+(g(x))^2$ とおくと

$$
h'(x)=\fbox{キ}h(x)
$$

これより

$$
\dfrac{d}{dx}(h(x)e^{-\fbox{キ}x})=\fbox{ク}
$$

がわかるので、

$$
h(x)=\fbox{ケ}e^{\fbox{コ}x}
$$

を得る。

解答形式

半角数字で改行区切りで記述せよ。たとえば $\fbox{ア}$ に $100$ , $\fbox{イ}$ に $-99$ と答えたい場合には１行目に $100$ , ２行目に $-99$ を記述せよ。

問題文

平面上に長方形 ${\rm ABCD}$ と点 ${\rm P}$ があり、 ${\rm AP}=11,{\rm BP}=9,{\rm CP}=3$ を満たしている。このとき ${\rm DP}$ の長さ $x$ を求めよ。

解答形式

半角数字で入力してください。

問題文

解答形式

「#」「%」「()」がそれぞれ「ある」「なし」のどちらであるかを、それぞれ一行目・二行目・三行目に答えてください。
それぞれの行は ある なし のいずれかで答えてください。