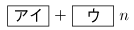問題文
$n$ を $2$ 以上の整数、$k$ を正の整数する。
$m$ の階乗を $m!$ とし、$m!$ を $n$ 進法で表したとき、末尾に連続して並ぶ $0$ の個数を $Z_n(m!)$ とする。
$Z_n(m!) = k$ を満たす最小の正の整数 $m$ を $M(n, k)$ とする。(そのような $m$ が存在しない場合、$M(n, k) = \infty$ とする。)
問:
$p$ を $5$ 以上の素数とする。
$A_p = M(p, p-1)$ と定義する。
このとき、
$$M(A_p, k_0) = p^3 - p^2$$
を満たす正の整数 $k_0$ が一意に存在するような、最小の素数 $p$ を求めよ。
また、対応する $k_0$ の値を答えよ。
解答形式
$p,k_0$をこの順に半角1スペースおきに書いてください。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています