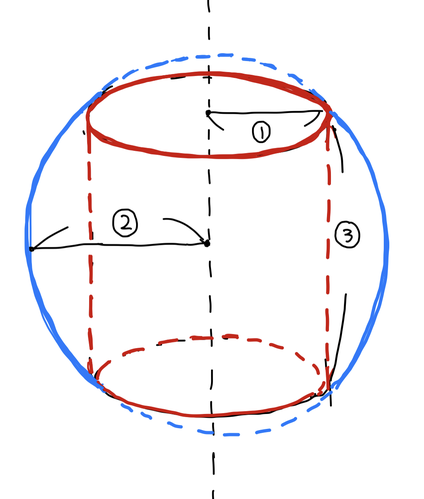
[D] monotonous decrease
2020年10月30日20:00
正解数: 9 /
解答数: 15
(正答率: 60%)
ギブアップ不可
この問題はコンテスト「Okapin Mathematical Contest 2」の問題です。
全 15 件
| 回答日時 | 問題 | 解答者 | 結果 | |
|---|---|---|---|---|
| 2024年12月16日18:46 | [D] monotonous decrease | ゲスト |
不正解
|
|
| 2024年12月16日18:34 | [D] monotonous decrease | ゲスト |
不正解
|
|
| 2024年2月29日22:24 | [D] monotonous decrease |
|
正解
|
|
| 2021年9月20日14:11 | [D] monotonous decrease | ゲスト |
不正解
|
|
| 2021年1月25日9:50 | [D] monotonous decrease |
|
正解
|
|
| 2021年1月25日9:50 | [D] monotonous decrease |
|
不正解
|
|
| 2021年1月25日9:49 | [D] monotonous decrease |
|
不正解
|
|
| 2020年11月9日21:05 | [D] monotonous decrease | ゲスト |
正解
|
|
| 2020年10月31日2:53 | [D] monotonous decrease |
|
正解
|
|
| 2020年10月31日2:30 | [D] monotonous decrease |
|
正解
|
|
| 2020年10月31日2:16 | [D] monotonous decrease |
|
不正解
|
|
| 2020年10月31日0:41 | [D] monotonous decrease |
|
正解
|
|
| 2020年10月30日23:18 | [D] monotonous decrease |
|
正解
|
|
| 2020年10月30日23:01 | [D] monotonous decrease |
|
正解
|
|
| 2020年10月30日22:07 | [D] monotonous decrease |
|
正解
|
おすすめ問題
この問題を解いた人はこんな問題も解いています