数学の問題一覧
公開日時: 2023年3月26日19:00 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
ある座標平面がある。
(6、2)(6、0)(8、0)(8、18)(0、18)(0、2)(0、0)をそれぞれ
点A B C D E F G とする。この時、四角形ABGFと六角形DCBAFEの面積をそれぞれ2等分する直線Lを引くことを考える。
直線Lのy切片の絶対値を求めよ。
公開日時: 2021年6月13日10:35 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
3つの半円が図のように配置されています。赤い線分の長さが$2\sqrt 2$のとき、青い線分の長さを求めてください。
なお、青い線分は2つの半円の中心間を結ぶ線分です。

※最大の半円と最小の半円の半径比は2:1。傾いた半円は最小の半円に接する。
解答形式
半角数字で解答してください。
公開日時: 2023年10月26日15:53 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
整数 整数問題
問題文
数列$a_n$を次のように定める。
$a_1=1$
$a_n=n^{a_{n-1}}$
このとき、以下の問いに答えなさい。
(1)$a_{2023}$の一の位はいくつか求めよ。
(2)$a_{2024}$の一の位はいくつか求めよ。
(3)$a_{2024}$の百の位はいくつか求めよ。
解答形式
(1) ~~~
(2) ~~~
の形でお願いします。問題番号と解答、一つの小問の解答と解答の間は半角スペースを開けてください。
解答は数字のみお書きください。
公開日時: 2021年5月16日2:37 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
図のような半円2つと正方形を組み合わせた図形があります。2つの半円弧に引いた接線が直交しているとき、図中の青で示した角の角度を求めてください。

解答形式
度数法で単位を付けずに0以上180未満の数を半角で解答してください。
例:$x=120°$であれば、120 と解答
公開日時: 2023年11月12日7:35 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
組み合わせ
$100\times 100$ のマス目があります. 上から $i$ 行目, 左から $j$ 列目のマスを $100(i-1)+j$ と呼ぶことにします. SMC 君は一般的な $6$ 面サイコロを $10000$ 回振り, $i$ 回目に振って出た目をマス $i$ に書き込みます. このとき, 以下の条件を満たす確率を $p$ とするとき, $6^{10000}p$ は整数になるので, 素数 $3299$ で割った余りを求めてください.
- 任意の行について, その行のマスに書かれた整数の総和は偶数.
- 任意の列について, その列のマスに書かれた整数の総和は $3$ の倍数.
公開日時: 2024年2月23日22:07 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
組み合わせ
$n$ を正の整数とする.縦 $3$ 行,横 $3$ 列からなるマス目の各マスに $n,n+1,\ldots,n+8$ を重複なく書き入れる方法であって,以下を満たすものの数を $f(n)$ とします.
- どの列,どの行についてもその $3$ つに書かれている $3$ 数を $3$ 辺の長さに持つ三角形が存在する.
ただし,回転や反転によって一致する数の書き込み方は,区別するものとします.$f(n)\lt3\times10^5$ を満たすとき,$f(n)$ としてあり得る最大の値を解答してください.
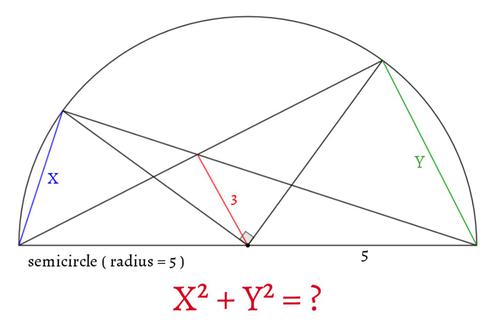
公開日時: 2020年9月8日19:11 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
図のように配置された図形で、半円の半径が$5$、赤、青、緑の線分の長さがそれぞれ$3,X,Y$のとき、$X^2+Y^2$の値を求めてください。
解答形式
半角数字で解答してください。
公開日時: 2022年12月4日22:11 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
初等幾何 角度

【補助線主体の図形問題 #081】
今週の図形問題は求角問題にしてみました。おそらく僕も想定していなかった解法がいろいろあることでしょう。想定解は補助線がビシッと活躍します。どうぞ思い思いの解法をお楽しみください。
※2022年12月6日22時17分追記
問題文に誤りがあり、修正したものに差し替えました。ここにお詫びして訂正いたします。申し訳ございませんでした。
(誤)接線AB、AC → (正)接線PB、PC
解答形式
${\renewcommand\deg{{}^{\circ}}}$ 解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。角度は弧度法ではなく度数法で表すものとします。
(例) $12\deg$ → $\color{blue}{12.00}$ $\frac{360}{7}^{\circ}$ → $\color{blue}{51.43}$
入力を一意に定めるための処置です。
近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。
公開日時: 2020年6月15日8:39 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
数列 $ \{ a_n \} $ $(n=1,2\dots)$ を、
$$
a_1=1,\ a_{n+1} = \sum_{k=1}^{n}\frac{8k-3}{4n^2-1}a_k\ (n = 1,2,...)
$$
で定める。$\displaystyle \lim_{n\to\infty}{a_{n}}$ を求めよ。
解答形式
求める極限値は、ある有理数 $q$ を用いて $q \pi$ と表せる。この $q$ を小数で表し、小数第4位を四捨五入したものを入力せよ。すべて半角数字で入力すること。なお、もし $3/2=1.5$のようになる場合は、$1.500$ と入力せよ。