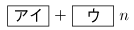問題文
※これは一般公開向けの問題ではありません.
この前の問題を思い出してください.
解答形式
問題の指示に従って解答を非負整数で入力してください.
正しくないジャッジ結果となるのを防ぐため,解答に空白文字を含まないようにしてください.
ヒント1
この問題に誘導があるとしたら以下の通りです.
ヒント2
(1)正方形の一辺の長さを求めよ.
ヒント3
(2)CDの長さを求めよ.
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています