C-3n畳神話大系
2020年6月28日18:00
正解数: 16 /
解答数: 23
(正答率: 69.6%)
ギブアップ不可
この問題はコンテスト「KOH Mathematical Contest #1」の問題です。
問題文
$n$ を非負整数とする。縦の長さが $3$,横の長さが $2n$ の長方形をした部屋を,辺の長さが $1$ と $2$ の長方形の畳で敷き詰める方法の総数を $a_n$ とする。ただし,部屋を固定したとき,畳を回転または反転させて一致するような敷き詰め方は区別して数える。また,便宜上 $a_0=1$ と約束する。
例えば,縦の長さが $3$,横の長さが $2$ である部屋を畳で敷き詰める方法は
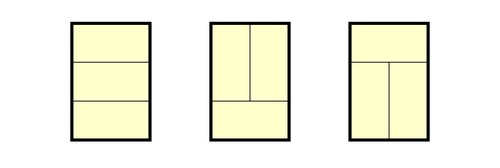 の $3$ 通りだから $a_1=3$ である。このとき
の $3$ 通りだから $a_1=3$ である。このとき
$$
a_n=\fbox{ア}\;a_{n-1}+\fbox{イ}\;\sum_{k=0}^{n-2}a_k\quad (n=2,3,\cdots)
$$が成り立つから
$$
a_4=\fbox{ウエオ}
$$である。また,上の漸化式を変形すると
$$
\lim_{n\to\infty}\frac{a_{n+1}}{a_n}=\fbox{カ}+\sqrt{\fbox{キ}}
$$が成り立つことが分かる。
解答形式
$\fbox{ア}$ 〜 $\fbox{キ}$ には,半角数字 0 - 9 のいずれかが当てはまります。$\fbox{ア}$ 〜 $\fbox{キ}$ に当てはまるものを,改行区切りで入力してください。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています