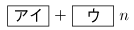データの分析・数列

問題文

$1$ から $30$ までの自然数が書かれたカードがそれぞれ $1$ 枚ずつの計 $30$ 枚ある。
この中から $1$ 枚を引き，書かれている数字を確認してから束に戻す操作を $11$ 回繰り返す。
この $11$ 回の操作で得られた自然数を小さい順にならべ，$A_{1}$ から $A_{11}$ とする。
$A_{1}$ から $A_{11}$ は以下の条件を満たしている。

＜条件＞
①　$A_{1}$ から $A_{11}$ は相異なる自然数である。
②　データの範囲は $27$ である。
③　データの四分位範囲 [$\mathrm{IQR}$] は $9$ である。
④　四分位数 [$Q_1,Q_2,Q_3$] はこの順に等比数列になっている。
⑤　中央値と平均値 [$\bar{A}$] の差の絶対値は $1$ である。
⑥　$A_7$ から $A_{11}$ までの $5$ つの数の和は $A_1$ から $A_5$までの $5$ つの数の和のちょうど $2$ 倍である。
⑦　$A_{1}$ から $A_{11}$ の中に立方数が $2$ つある。
⑧　このデータのうち四分位数を除いた $8$ 個の数字を $2$ つずつに分けてできた $4$ つの数字の組
　　$(A_1,A_2),(A_4,A_5),(A_7,A_8),(A_{10},A_{11})$ について、それぞれの組に $1$ つずつ素数がある。
⑨　このデータには外れ値が $1$ つ存在する。ただし外れ値は以下の通りに定義する。
　　 [$Q_1-1.5 \times \mathrm{IQR}$ 以下　または　$Q_3+1.5 \times \mathrm{IQR}$ 以上]

問　このデータの要素を決定せよ。

解答形式

$A_1$ から $A_{11}$ までの11個の自然数を半角空白区切りで1行で回答

投稿者より

数学の問題というよりパズルっぽくなってしまいましたが，作るのが大変だったので供養。
問題の不備、解説に不十分なところ、冗長なところなどありましたら，
コメントで教えてくださるとありがたいです。

解説は最初から誰でも見られるようになっていますが，少し長いです。

本当はこの後，状況設定的に確率・場合の数の問題を入れようとしてたが，大変なので一旦おしまい。
気が向いたら続きをつくるます。