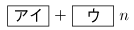与えられた等式
1 + 2 + 3 + ⋯ + 𝑛 = 𝑛² − ( 1 + 2 + 3 + ⋯ + ( 𝑛 − 1 ) ) が成り立つことを示す。
まず、左辺と右辺をそれぞれ計算する。
左辺の和は、等差数列の和の公式を用いると、
1 + 2 + 3 + ⋯ + 𝑛 = 𝑛 ( 𝑛 + 1 ) / 2である。
同様に、右辺、 1 + 2 + ⋯ + ( 𝑛 − 1 ) の和は、 ( 𝑛 − 1 ) 𝑛 / 2
よって、右辺は (𝑛² − ( 𝑛 − 1 ) 𝑛 )/ 2
これを計算すると、
(2 𝑛 ² − ( 𝑛 − 1 ) 𝑛) / 2 =( 2 𝑛 ² − 𝑛 ² + 𝑛) / 2= (n² + n) / 2= n (n + 1) / 2
よって左辺＝右辺となる。 Q.E.D.