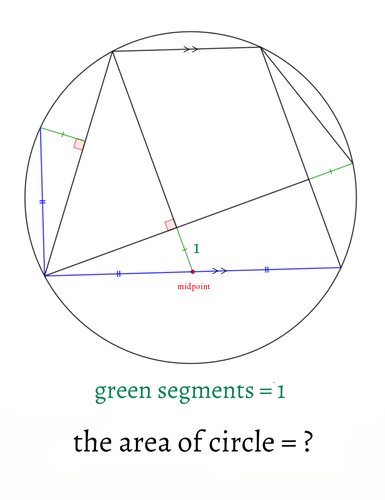
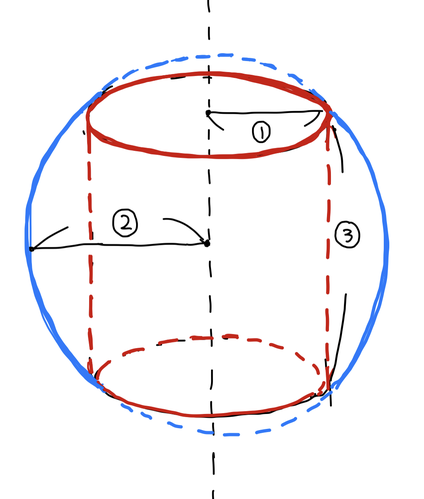
問題文
全長 $L$ mのリムジンが、下図のように直角に曲がったトンネルを、幅 $a(>0)$ mの道から幅 $b(>0)$ mの道へ曲がろうとしている。
このとき、リムジンがトンネルを曲がることのできる最大の全長 $L_{max}$ (m)を求めよ。なお、車の全幅は考えなくて良いものとする。
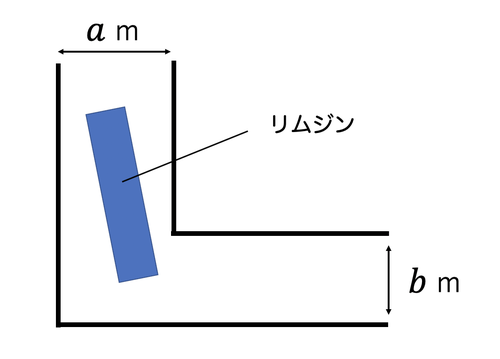
解答形式
$a=5,b=6$のときの$L_{max}$の値を関数電卓を用いて計算せよ。答えは、小数第4位の数字を四捨五入したものを解答せよ。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています