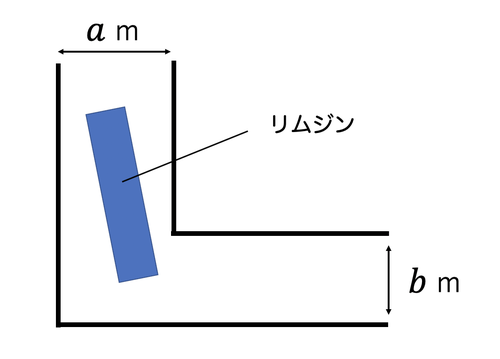
問題文
関数
$f(x)=\sqrt[3]{-(x+4)(2x+3)(3x-8)}\ \left(\displaystyle -\frac{3}{2} \leq x \leq \frac{8}{3}\right)$
の最大値を求めよ。
解答形式
半角数字またはTeXを入力してください。
ヒント1
無意識に微分しようとせず、他の方法を考えましょう。
ヒント2
マイナスをどこに分配するとxの係数である1,2,3を活かせますか?
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています