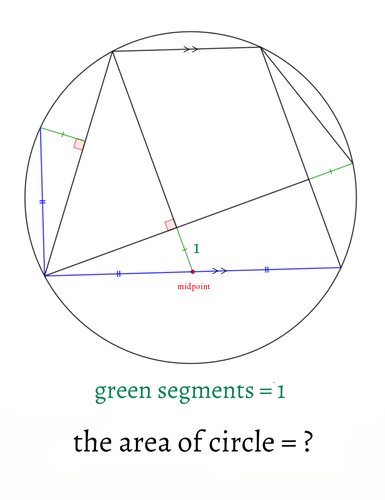
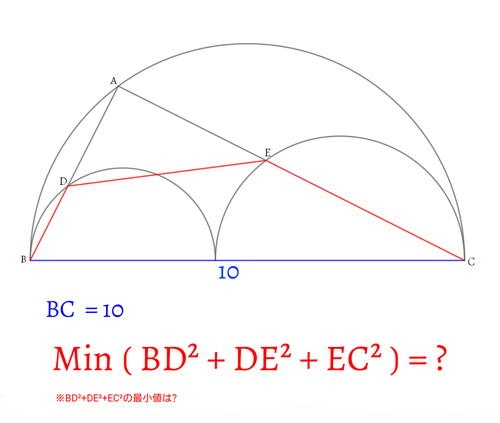
問題文
$n$ を整数とする。$x$ の整式
$$
x^4+(3n+2)x^3+(n^2+5)x^2+nx-1
$$
が整数係数の範囲でさらに因数分解できるような $n$ をすべて求めよ。
解答形式
$n$の値を小さい順に1,2,3,......行目にすべて半角で入力せよ。たとえば $n=-123, 45, 678$ と解答する場合、1行目に「-123」、2行目に「45」、3行目に「678」と入力せよ。
ヒント1
まず何をすればよいかわからない場合は、ヒント2を見よ。
解は3つ存在する。2つしか見つからない場合は、何か見落としがないか考えてみよ。
3つめの解の手がかりがどうしても見つからなければ、ヒント3を見よ。
ヒント2
定数項が $-1$ であることに注目せよ。整数係数の因数分解であることに注意せよ。
ヒント3
2次式どうしの積で表される場合を見落としていないだろうか。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています