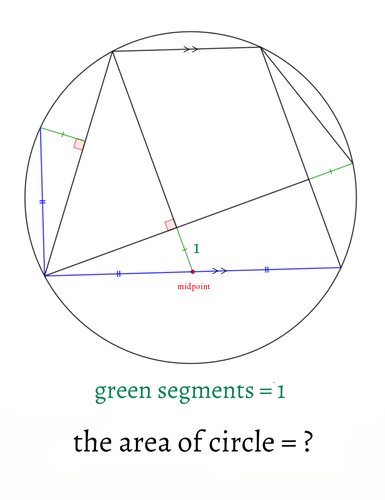
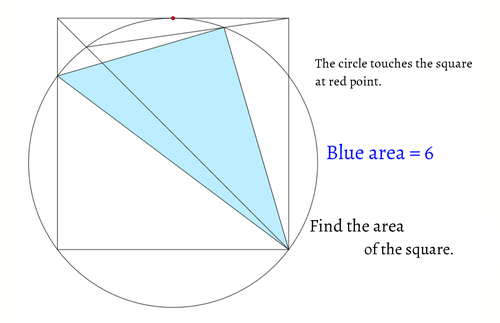
問題文
$f_m(x)$という関数列を$f_1(x)=\log{x},f_{m+1}=\log{f_m(x)}$と定義します。ただし$\log{x}$は自然対数です。
具体的には$f_1(x)=\log{x},f_2(x)=\log{\log{x}},f_3(x)=\log{\log{\log{x}}},\ldots$となります。
このとき、
$$\lim_{n\to\infty}\{f_m(3^n)-f_m(2^n)\}=0$$
となるような最小の自然数$m$を求めてください。
解答形式
半角数字で入力してください。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています