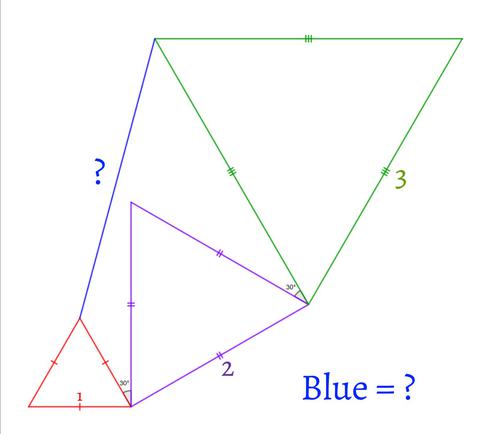
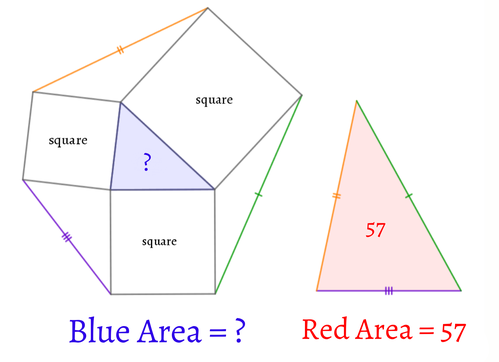
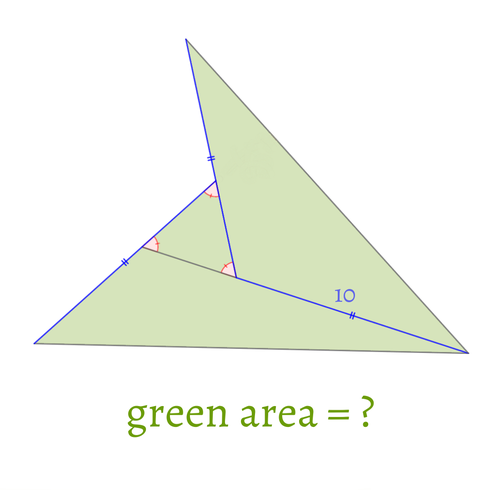
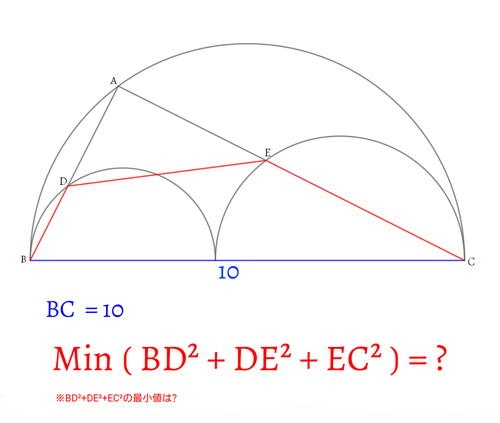
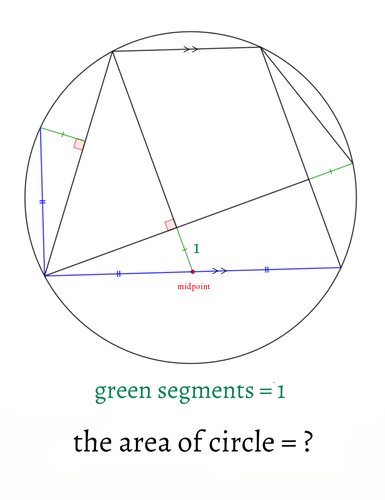
問題文
$1\thicksim6$までの数字を$1$回ずつ使って空欄を埋め以下の等式を成立させてください。解が存在しない場合はその旨を答えてください。
$(1)\square\square\times\square=\square\square\square$
$(2)\square\square+\square\square=\square\square$
解答形式
1行目に$(1)$、2行目に$(2)$の解を入力してください。
等式をすべて半角で入力してください。ただし、「$\times$」はx(小文字のエックス)で代用するものとします。
存在しない場合は-1を入力してください。
また、解が複数存在する場合はどれを回答してもかまいません。
(例)
$3\times7=21$と入力する場合 3x7=21
$3+7=21$と入力する場合 3+7=10
ヒント1
値を上から抑えたり、一の位に注目したり、総和に注目することで解を絞り込めます。
ヒント2
候補は高々210通りしかないので、全探索するのも手です。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています