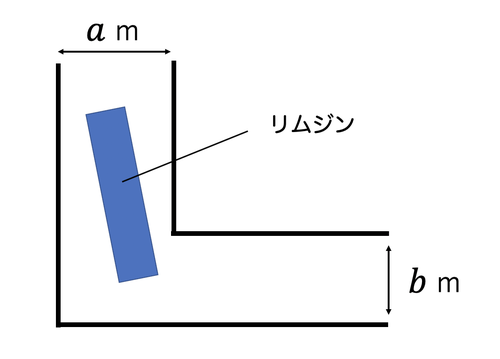
問題
(1) $a,b$ を整数でない正の有理数とする。 $a^b$ は常に無理数か。
(2) $a$ を整数でない正の有理数とする。 $a^a$ は常に無理数か。
(3) $a,b$ を正の無理数とする。 $a^b$ は常に無理数か。
(4) $a$ を正の無理数とする。 $a^a$ は常に無理数か。
解答方法
解答欄に改行区切りで O (オー)または X (エックス)を記述せよ。正解判定は各行に対して行われ、完答のみ正解となる。
解答提出
スポンサーリンク
おすすめ問題
この問題を解いた人はこんな問題も解いています
問題文
ある大きさの球から、ある直径の円柱をくりぬいた。円柱の軸は球の中心を通る。（ビーズのような形を想像してください）
この立体の体積が$36\pi$のとき、以下のうちいずれかの値が一意に定まる。
- 円柱の底面の半径
- 球の半径
- 円柱の深さ
一意に定まるものの番号と、その値を求めよ。
解答形式
一意に定まるものの番号を半角数字で1行目に、その値を2行目に入れてください。2行目は整数または既約分数で答えてください。
解答例
1
4
問題文
1円, 5円, 10円, 50円, 100円, 500円の硬貨が1枚ずつある。1回目の試行で6枚の硬貨を投げ、表が出た硬貨をもらうことができる。2回目の試行では、残った硬貨を投げ、やはり表が出た硬貨をもらうことができる。もらえる金額が600円以上になったらこの試行は終了するものとする。
(1) 1回目の試行で終わる確率はいくらか。
(2) 2回目の試行で終わる確率はいくらか。
解答形式
(1)の答えを1行目に、(2)の答えを2行目に既約分数で入れてください。
解答例
1/2
3/10
問題文
緑色の線分の長さは１です。
このとき、円の面積を求めてください。
図中の赤点はそれを含む線分の中点です。
解答形式
答えは(分数)×πの形になります。
分子を１行目に、分母を２行目に半角数字で入力してください。
ただし、既約分数の形で解答してください。
例: (10/3)π → １行目に10、２行目に3
問題文
※解答形式に注意!
図のように配置された3つの正三角形があります。青い線分の長さを求めてください。
ただし、赤、紫、緑の線分の長さはそれぞれ1，2，3で、隣り合う正三角形の間の角は30°です。
解答形式
答えは自然数$A,B$を用いて$A\sqrt{B}$の形に表せます。$A+B$を解答してください。
ただし、根号の中はできるだけ小さい自然数にしてください。
問題文
$n\;(\geq 2)$ を自然数とするとき，以下の試行を行うことを考える。
試行
- $n$ 人が $0,1,2$ のいずれかひとつの数を無作為に選ぶ。
- 人 $i\; (i=1,2,\cdots, n)$ が選んだ数を $a_i$ とする。各人 $i$ に対して，
$$
a_i\equiv\sum_{j=1}^n a_j\; ({\rm mod} \; 3)
$$ならば人 $i$ は生存し，そうでないなら脱落する。この試行をmodじゃんけんと呼ぶことにする。
$n$ 人がmodじゃんけんを $1$ 回行い，全員が生存するか全員が脱落するとき，modじゃんけんの結果はあいこになると定義する。
$n$ 人がmodじゃんけんを $1$ 回行ってあいこになる確率を $p_n$ とするとき
$$
p_2=\frac{\fbox{ア}}{\fbox{イ}},\; p_3=\frac{\fbox{ウ}}{\fbox{エ}},\; p_4=\frac{\fbox{オ}}{\fbox{カキ}}
$$
である。$n$ を $\fbox{ク}$ で割った余りが $\fbox{ケ}$ であるとき
$$
p_n=\frac{\fbox{コ}^{n}+\fbox{サ}}{\fbox{シ}^n}
$$
であり，そうでないときには
$$
p_n=\frac{\fbox{コ}^{n}+\fbox{ス}}{\fbox{シ}^n}
$$
である。また，
$$
\lim_{n\to\infty} p_n=\fbox{セ}
$$
が成り立つ。
解答形式
空欄 $\fbox{ア}$ 〜 $\fbox{セ}$ には，半角数字 0 - 9 または記号 - のいずれかが当てはまります。$\fbox{ア}$ 〜 $\fbox{セ}$ に当てはまるものを改行区切りで入力してください。分数はこれ以上約分できない形で解答してください。
問題文
原点$O$とする$xy$平面上で点$(3,2)$を通る傾き負の直線と$x$軸,$y$軸との交点をそれぞれ$A,B$とするとき、$\triangle OAB$の面積の最小値を求めよ。
解答形式
整数または既約分数で答えてください。
半角で入力してください。
問題文
以下のような数列 $\{a_n\}$ を考える。
$$
a_n=1+\sum_{m=1}^{2^n}{\rm floor}\left[\sqrt[n]{\frac{n}{\displaystyle{\sum_{k=1}^m}\; {\rm floor}\left(\cos^2\cfrac{(k-1)!+1}{k}\pi\right)}}\right]
$$なお、${\rm floor}(x)$ は $x$ 以下の最大の整数を返す関数とする。このとき、$a_{20}$ を求めよ。
ただし、必要であれば以下の定理および不等式を用いても良い。
- $n$ が素数のとき
$$\quad(n-1)!\equiv-1 \pmod n$$ - $n\geq 1$ のとき
$$1\leq\sqrt[n]{n}<2$$
解答形式
半角数字で入力してください.
問題文
(1)$p$を奇素数とし、$\frac{1}{p}$を2進数で表示したときの循環節(※)が2以上8以下であるような$p$は6つ存在する。フェルマーの小定理を用いて$p$とその$p$に対する$\frac{1}{p}$の循環節の長さの関係を導き、6つの$p$の値を全て答えよ。
(2)$p$を奇素数とし、$\frac{1}{p}$を2進数で表示したときに最大で1が連続して並ぶ個数を$f(p)$とおく。例えば$\frac{1}{3}=0.01010…_{(2)}$より$f(3)=1$である。(1)を満たす$p$の中で$f(p)$が最大となるのは$p$がいくらのときか。Midyの定理を用いることによって求め、その値を答えよ。
(※)循環節とは、循環小数の繰り返される数字の列のうちその長さが最小でありかつその先頭が最も先に来るようなもののことである。例えば$\frac{1}{3}=0.01010…_{(2)}$となり、このときの循環節は$01$であり、$0101$や$10$は循環節とならない。
解答形式
(1)の全ての答えを小さい順に1~6行目に半角数字で入力してください。また、(2)の答えを7行目に半角数字で入力してください。
問題文
おかぴんはチョコレート入りの袋が3袋入った箱を持っていて、これから食べようとしています。
しかし、おかぴんは怠惰なので食べ終わった空の袋を捨てずに、再び箱の中に入れてしまいます。
箱の中から1袋ずつ取り出して、それがチョコレートの入った袋だったなら食べて箱の中に空の袋を戻し、それが空の袋だったなら食べずにそのまま箱の中に戻す、という試行を繰り返します。
チョコレートの入った袋を取り出す確率も空の袋を取り出す確率も同様に確からしいとするとき、箱の中の全てのチョコレートを食べ終えるまでの試行回数の期待値を求めてください。
解答形式
答えは$\frac{\fboxア}{\fboxイ}$(ただし既約分数)となります。$\fboxア\fboxイ$に入る数字をそれぞれ1,2行目に半角で入力してください。
※計算が大変なのでwolframalpha等で計算してください。
問題文
$k$を$0$以上の実数, $e$を自然対数の底とする。数列$a_n$を
$$a_n=\frac{n!e^n}{n^{n+k}}$$
と定める。任意の自然数$n$に対して, $a_{n+1} < a_n$が成り立つような最小の$k$を求めよ。
解答形式
整数または既約分数で答えてください。
